空间域中的图像处理是处理像素操作技术的视觉丰富的研究领域。对图像执行不同的操作,这些图像被简单地视为二维数组。
通常,所有这些基于矩阵的操作都在较大矩阵(代表完整图像)和较小矩阵(称为 2D 内核)之间执行。内核大小和相关值决定了它对所考虑图像的影响。
例如,假设我们有一个矩阵 [0 1;-1 0] 并将其与图像进行卷积,如图 1(a) 所示;结果将如图 1(b) 所示。我们可以看到卷积操作导致了图中普遍存在的边缘的确定。然而,得到的结果是不完整的,因为我们还没有完整的边集。
为了得到剩余的边集,我们需要再进行卷积运算。但是这次我们的内核将是 [0 -1;1 0] 而不是 [0 1; -1 0]。由此产生的边缘如图 1(c) 所示。

在此之后,我们需要结合上述两个操作的结果以获得图像中存在的所有边缘(图 1(d))。提到的这对内核被命名为罗伯茨内核,对原始图像执行的整个操作被称为罗伯茨边缘检测。
另一方面,如果内核大小为 3×3,每个元素的值为 1/9,则其与图像的卷积会使图像平滑,如图 2 所示。也就是说,生成的图像在与原来的比较。该操作称为平滑,内核称为平滑器。
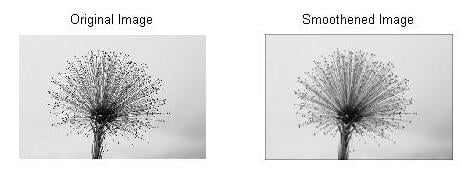
在这里的任何一个例子中,我们都看到了一个共同的因素——“卷积”。卷积在这些例子之外还有更多的图像处理应用,被认为对图像处理操作很重要。
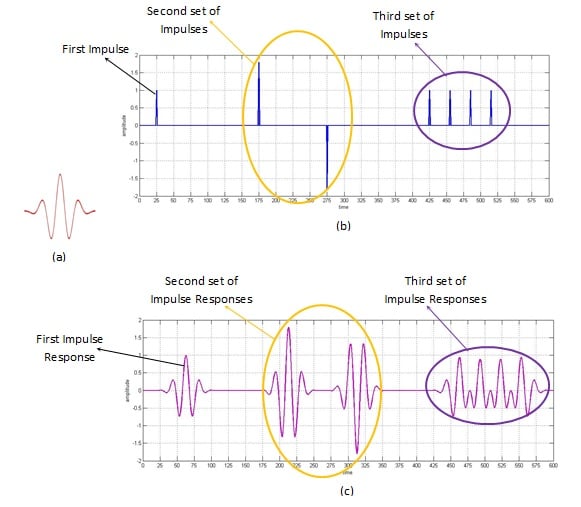
考虑一个系统,其脉冲响应(单位脉冲输入的系统输出)如图 3(a) 所示。现在,假设我们希望此模式出现在时刻t = 25。
为了实现这一点,我们需要一个在t = 25 时具有脉冲的输入信号。系统输入端存在脉冲(图 3(b) 中所示的“脉冲”)导致出现系统在该特定时刻的脉冲响应(在图 3(c) 中显示为“脉冲响应”)。
如果我们希望我们的脉冲响应在按 1.8 倍缩放后出现在t = 175,那么我们需要在输入端按相同数量缩放的脉冲响应出现在t = 175。
更进一步,假设我们想在t = 275 时反转它。那么我们需要在同一时刻有一个反转的脉冲。相关波形分别由图 3(b) 和 3(c) 的第二组脉冲和相关响应显示。
基于同样的理由,我们可以猜测,如果我们希望拥有一个间隔为t = ' a ' 单位的系统响应序列,那么,我们可以通过用脉冲序列激励系统来获得它间距也是' a '时间单位。
但是,请注意脉冲间间距。为了忠实复制,必须确保样本之间有足够的间距,否则会出现失真。
例如,如果系统的脉冲响应跨越 ' s ' 个时间单位的持续时间,则输入信号中样本之间的间隔必须大于或等于 ' s' 个时间单位。低于此值的任何值都会导致样本重叠,从而影响输出。这可以在图 3(c) 的一部分(第三组)中观察到,它显示了失真的输出,因为脉冲序列(在图 3(b) 中显示为第三组脉冲)以 30 倍的间隔间隔开瞬间,而脉冲响应(在图 3(a) 中)本身跨越大约 75 个时间单位。
该图表明我们可以通过使用卷积来合成定制的输出模式,前提是它只需要重复系统以缩放或未缩放的方式响应。
y[n]=N∑k=0h[k]x[nk]
其中y [ n ] 是将输入信号x [ n ] 通过系数为h [ n ]的滤波器获得的输出。
这里,求和的范围从 0 到N,因为我们的h [ n ] 信号本质上是有限的。
但是请注意,即使我们将限制更改为超出此范围,过滤器也不会受到影响。假设我们从k = -2 到N + 5 (而不是 0 到N)求和。即便如此,我们的输出仍然保持不变。这是因为h [ n ]的值对于k = -2 到 0 和N到N + 5 将为零,这意味着总和也将为零。
推广这一点,我们甚至可以将 FIR 滤波器的方程式写成(只是为了方便)
细看。你觉得这很熟悉吗?您可能将其视为数字卷积方程(如 第 I 部分中所讨论)。
这是什么意思?过滤和卷积一样吗?答案是肯定的——前提是我们的脉冲响应函数与滤波器函数相同。
即使当我们考虑 IIR(无限脉冲响应)滤波器时,同样的类比也适用。然而,有一个例外,这次我们需要将输入信号和过去的输出信号与它们各自的系数进行卷积。
简而言之,卷积构成了信号过滤成功的基础(即使在二维图像的情况下)。
考虑我们想要将两个多项式相乘的情况,比方说,(2 x 2 + 3 x – 1) 和 (3 x 3 – 2 x )。用于实现此结果的工作如下所示
(2 x 2 + 3 x – 1) × (3 x 3 – 2 x ) = 6 x 5 - 4 x 3 + 9 x 4 - 6 x 2 - 3 x 3 + 2 x
= 6 x 5 + 9 x 4 - 7 x 3 - 6 x 2 + 2 x
现在,让我们形成两个数组,其元素是所提到的多项式的系数,然后对它们进行卷积。在此示例中,数组将为数组 1 = A 1 = {2, 3, -1} 和数组 2 = A 2 = {3, 0, -2, 0}。
我们将使用乘加技术对它们进行卷积,如表 1 所示,您可以在 本系列文章的 第 I 部分中了解相关内容。
从表中可以看出,他们的卷积结果是{6, 9, -7, -6, 2, 0}。以多项式形式表示,这等同于等式 1 中所示的内容。
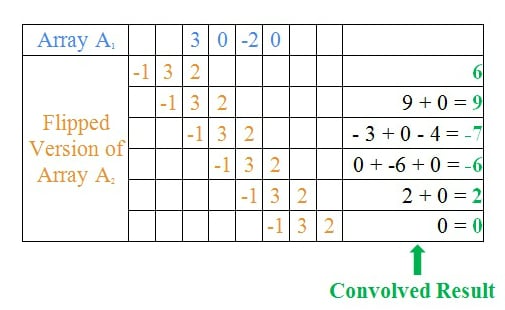
结果表表明,当我们将两个多项式相乘时,我们实际上是从数学角度对它们的系数进行卷积。这巧妙地证明了卷积有助于我们执行多项式的乘法。
礼堂、电影院和其他类似建筑在很大程度上依赖于混响的概念, 因为它大大提高了声音的质量。
数字模拟混响的过程在技术上称为“卷积混响”。使用卷积混响,您可以将一个区域的已知脉冲响应与所需声音的脉冲响应进行卷积,以模拟特定区域的混响效果。
通过这样的模拟,我们可以做一些很酷的事情:我们可以在不亲临现场的情况下计算出礼堂的声学效果对小提琴演奏的影响。使用这种技术的另一种方法是合并两种声音——比如,歌手的声音和维纳琴的声音,以产生一种新的声音。
神经网络是人工智能的一个领域,它通过模仿人脑中的连接来设计电路。大脑内神经元之间的互连被建模为构成网络的多层节点之间的互连。

图 4 显示了这种简单形式的人工神经网络 (ANN)。该示例有一个隐藏层,它将输入节点路由到输出节点。节点显示为圆形区域,而蓝线表示互连。
在这样的网络中,每个互连都与一个称为权重的参数相关联。这些权重表示特定节点对特定输出的影响程度。一些神经网络还包含卷积——它们被称为卷积神经网络,它们是图像处理的强大工具。
地震学是地球物理学的一个分支,主要研究地震和其他弹性波穿过地球甚至其他行星的情况。地震波可以穿过地球的不同层,每一层都有自己的成分和反射率。将所有反射波相加可以得到净反射波。由此产生的图表在技术上被称为“合成地震图”。
将特定地球层的反射系数与输入信号相乘,然后将所得波相加的行为可以通过卷积运算有效地建模。换句话说,我们可以说地球的反射率系列,可以被认为类似于地球的脉冲响应,可以在与入射地震波卷积时呈现合成地震图(石油勘探中的地震建模和模式识别) .
当准直光通过其中有狭缝的孔径时,光会沿着不连续点发生衍射。该行为导致在位于无穷远的平面上形成sinc函数,这被称为穿过狭缝的光的衍射图案。同样,对于圆形孔径,由此产生的衍射图案将是一个草帽函数(成像光谱仪简介)。
现在,假设我们有一个光圈,它是这两种形状(狭缝和圆形)的组合。我们能否在不实际重复该过程的情况下得出这种复杂结构的衍射图样?我们可以。事实上,生成的模式将是通过将 sinc 函数与 sombrero 的函数进行卷积而获得的模式。
这表明,当我们知道每种孔径的衍射图案时,可以通过对这些单独的图案进行卷积来获得它们组合的衍射图案。卷积可以帮助简化的大多数线性系统都表现出类似的叠加行为。
让我们考虑这样一种情况,我们有两个独立的随机变量 X和Y,它们的概率密度函数 (pdf)分别为f和g。如果我们希望计算它们之和的 pdf(即,如果我们需要X + Y的 pdf ),我们可以使用f和g 的卷积。
继续这个逻辑,我们可以计算任意数量的独立变量之和的 pdf。这很重要,因为许多标准分布的特点是简单的卷积模式,这意味着我们可以使用卷积找到它们的 pdf。
层析成像是一种获取物体特定平面图的技术。使从源产生的窄束 X 射线(或任何其他类似的穿透辐射)穿过所需的物体。然后这些射线被通常放置在物体另一侧的探测器收集。
生成的图像是源光线与物体成分的卷积,揭示了其内部结构。但是,生成的图像质量相对较低。
现在考虑一种情况,其中源和检测器组件沿物体的不同角度位置平移。此行为在同一预期平面上创建对象的多个视图。接下来,这些视图将通过 CT 重建算法进行处理,以获得高质量的图像。
卷积在使用重建算法的这一点出现。两种广泛使用的重建算法是 过滤反投影,它利用了卷积。
本文讨论了卷积运算在各个领域的使用,目的是突出其重要性。请随时在下面的评论中分享卷积的其他用途。
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。