使用线性延迟模型在 VLSI 设计中调整晶体管大小

时间：2023-04-10

在我们关于 VLSI 中的晶体管大小调整系列的续篇中，我们将介绍我们系列中的第三个也是一个模型，即线性延迟模型。如果您想了解线性 RC 延迟模型和流行的Elmore 延迟模型，请务必查看之前的文章。

线性延迟模型提供了一种更简单的方法来模拟大型 RC 分布式电路的延迟，正如我们在上一篇文章末尾观察到的那样，Elmore 延迟变得复杂或不准确。

在本文中，我们将学习如何找到较大电路中晶体管/逻辑门的尺寸以提供所需的性能。

线性延迟有什么作用？

回想一下上一篇文章，我们使用 Elmore 延迟将等效 RC 电路模型线性化为：

tpd=(p+gh)3RC $t_{p d} = (p + g h) 3 R C$

其中 p = 寄生延迟。

$h = fanout = \frac{输入电容}{输出电容}$

$g = 逻辑努力$

通过这个表达式，我们可以计算出多级 MOS 电路的尺寸。

什么是逻辑努力？

逻辑功是栅极的有效输入电容与反相器的输入电容之比。从这个意义上说，有效电容意味着输入端出现的电容。

查看下图所示的反相器，其中 PMOS 的单位尺寸是 NMOS 的两倍，以提供相等的上升/下降时间。

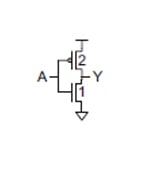
图 1.单元逆变器电路。所有图像改编自 CMOS VLSI 设计（第 4 版）1 ，作者 Neil HE Weste 和 David Money Harris

$逻辑努力 (g) = \frac{有效电容}{逆变器的有效电容} = \frac{3 C}{3 C} = 1$

对于下图所示的 3 输入与非门，输入 B 处的电容为 (3C + 2C = 5C)。

图 2. 3 输入与非门

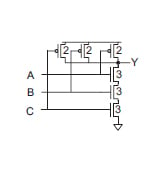
因此合乎逻辑的努力是

$逻辑努力 (g) = \frac{有效电容}{逆变器的有效电容} = \frac{5 C}{3 C} = \frac{5}{3}$

这与上一篇文章中推导出的线性化延迟是一致的

$t_{p d} = (1 + h) 3 R C$ 对于逆变器

$t_{p d} = (5 + \frac{5}{3} h) 3 R C$ 对于 NAND

如果您应用相同的技术，下图中所示的 3 输入或非门将给出 $\frac{7}{3}$ 的逻辑结果。

图 3. 3 输入或非门

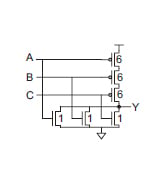
这种方法可用于计算其他常见逻辑门的逻辑努力，如下表所示。

表 1. 普通门的逻辑努力

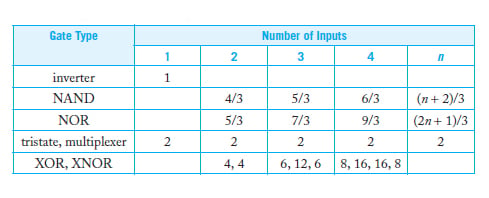
可以使用上一篇文章[链接]中描述的 Elmore 延迟或通过仿真来计算寄生延迟。为了简要总结寄生延迟的影响，考虑一个 N 输入 NAND 门，它的 Elmore 延迟等效值在下图中给出；

图 4. N 输入与非门和 RC 等效电路

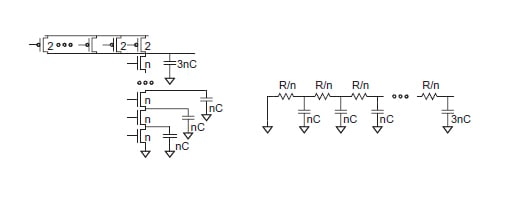
埃尔莫尔延迟是，

$t_{pd}=R(3nC)+ \sum_{i=1}^{n-1}(\frac{iR}{n})(nC)=\left ( \frac{n^2}{ 2}+\frac {5}{2}n \右 )RC$

从表达式中可以看出，寄生延迟部分随串联晶体管的数量(n)呈二次方增加，这就是为什么建议级联两个较小的门以形成较大的门以减少门的输入寄生延迟。在多级逻辑网络中可以进一步观察到这一点的含义，它是路径中每延迟的总和，如下图所示的多级逻辑网络所示。

图 5.多级逻辑网络

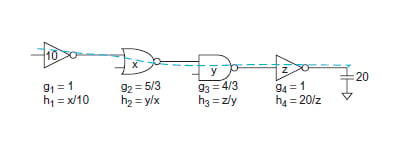
\[D=\sum{d_i} \; \;\textit{在哪里} \; \; d_i= g_ih_i+p_i\]

$D = \sum g_{i} h_{i} + \sum p_{i}$
\[D=\sum{g_ih_i} + P \;\; \textit{哪里} \; g_ih_i = \textit{舞台效果}\]

$F = \prod f_{i} = \prod g_{i} h_{i} = G H （舞台效果）$

路径电功 H 是路径的输出电容与路径的输入电容之比。

$H = \frac{输出电容}{输入电容} = \prod h_{i}$

路径努力 F 是每个阶段的阶段努力的乘积。由于目标是达到延迟值，因此每个阶段将为 n 阶段关键路径贡献等量的阶段努力。要求每个阶段必须具有相等的阶段努力。因此，对于 N 级网络，级工作量很简单；

$f_{i} = F^{\frac{1}{N}}$ -----阶段努力

所以，

$\sum g_{i} h_{i} = N f_{i}$

因此延迟表达式可以写成

$d = N F^{\frac{1}{N}} + P$

为了更好地理解这个概念如何应用于实际系统，我们将考虑通过逆变器驱动 64 个电容单位所需的功能单元。了解逻辑工作量后，我们可以确定阶段数以提供延迟。

图 6.反相缓冲器不同级数的比较

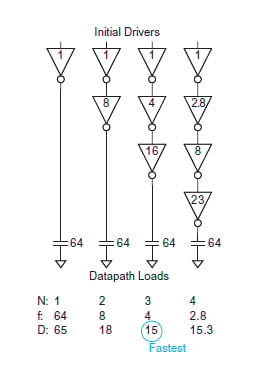
请注意，反相器的寄生延迟 $p_{i}$ 为1，因此对于N级反相器链网络，路径的总寄生延迟P将是每个反相器的寄生延迟之和，即N。

N = 1	N = 2	N = 3	N = 4
$Recall, d = N F^{\frac{1}{N}} + P$	$Recall, d = N F^{\frac{1}{N}} + P$	$Recall, d = N F^{\frac{1}{N}} + P$	$Recall, d = N F^{\frac{1}{N}} + P$
$P = \sum p_{i} = N = 1$	$P = \sum p_{i} = N = 2$	$P = \sum p_{i} = N = 3$	$P = \sum p_{i} = N = 4$
$F = G H = \frac{64}{1} = 64$	$F = G H = \frac{64}{1} = 64$	$F = G H = \frac{64}{1} = 64$	$F = G H = \frac{64}{1} = 64$
$f_{i} = 64^{\frac{1}{1}} = 64$	$f_{i} = 64^{\frac{1}{2}} = 8$	$f_{i} = 64^{\frac{1}{3}} = 4$	$f_{i} = 64^{\frac{1}{4}} = 2.83$
$d = (1) 64^{\frac{1}{1}} + 1$	$d = (2) 64^{\frac{1}{2}} + 2$	$d = (3) 64^{\frac{1}{3}} + 3$	$d = (4) 64^{\frac{1}{4}} + 4$
$d = 65$	$d = 18$	$d = 15 ()$	$d = 15.3$

由于三级反相器设计是延迟的设计，因此我们要确定每反相器的大小以给出延迟。

由于每个阶段的努力 $f_{i} = 4$ ，因此靠近负载电容的个反相器的大小为，

$F I = \frac{64}{C_{i n}}, C I N = \frac{64}{4} = 16 UNIT$

中间反相器导出为 $F I = \frac{16}{C_{i n}}, C I N = \frac{16}{4} = 4 UNIT$

虽然输入端个反相器的大小推导为，

$F I = \frac{4}{C_{i n}}, C I N = \frac{4}{4} = 1 UNIT$

每个阶段的总结如上图 6 所示。可以观察到，单级逆变器网络提供了的延迟，即使电路的整体尺寸，设计也会运行得非常慢。虽然 3 级设计的面积更大，但它为设计提供了延迟量，从而使系统按照规范工作。

至此，我们已经能够研究MOS电路中的各种延迟模型。虽然这些方法简单且相当准确，但在准确性至关重要的情况下，它们不能完全替代 CAD 工具。然而，这些方法适合提供一种快速而粗略的方法来深入了解各种电路拓扑和关键路径设计。

上一篇：针对高压应用优化宽带隙半导体器件

下一篇：构建一个 Arduino 控制的 USB 电源