每个 PWM DAC 设计都需要模拟滤波,以将所需的 PWM 占空比成比例的直流分量与不需要的交流纹波分开。其中简单的是基本的 RC 低通
滤波器,它提供峰峰值纹波幅度(对于 50% PWM 占空比的坏??情况,其中 T PWM = PWM 周期时间,并假设 RC > T PWM)的:
V纹波/ V满量程= T PWM / 4·RC
明显的设计权衡是,虽然可以通过选择足够大的 RC 产品来实现任何所需程度的纹波衰减,但稳定时间会相应受到影响。例如,如果我们(相当合乎逻辑地)选择稳定带的定义等于纹波幅度,那么……
T settle = RC·ln(V fullscale / V ripple )
= T PWM ·V fullscale ·ln(V fullscale / V ripple ) / (4·V ripple )
这种关系的后果可以用 8 位的情况来说明:
给定:V纹波/ V满量程= 1/256;RC = 64·T脉宽调制
T稳定= 64·ln(256)·T PWM = 355·T PWM
其中,即使对于相当快的 32 kHz(31?s T PWM),也预测了 11 毫秒的稳定时间。
显然,如果稳定时间是一个关键的设计参数,我们就需要做得更好,找到一种不太简单的滤波方案。我之前的 DI,Fast-settling synchronous-PWM-DAC
filter has almost no ripple说明了这个方向的极端可能性。
但并非所有不能容忍一月糖蜜355·T PWM 稳定时间的应用都需要或能够证明这种复杂的滤波解决方案是合理的。此处介绍的设计理念解决了这些中间应用程序。如图1所示,它通过一个反相器、R2 和 C2 增强了基本的 R1/C1 低通,它们结合起来从需要的直流信号中抵消和减去(大部分)不需要的交流分量,留下相对干净的模拟稳定时间比简单的 RC 滤波器少得多的输出。
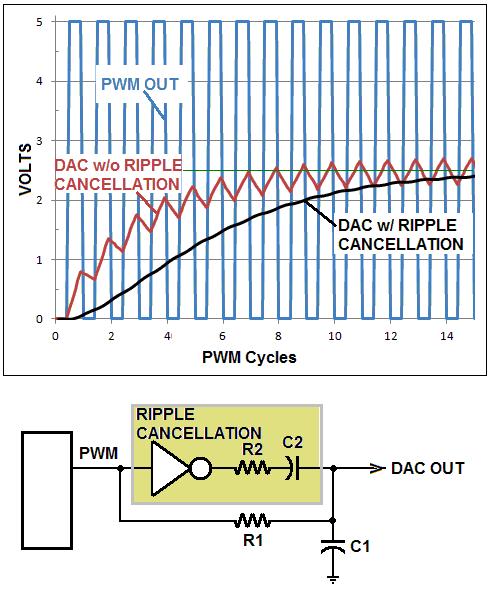
图 1 PWM DAC 纹波
消除器的波形和原理图
但“相对干净”有多纯,“少得多”有多快?设置 R2=R1 和 C2=C1,新电路的纹波和稳定时间数据为:
Vripple / Vfullscale = (TPWM / 4·RC)2
Tsettle = TPWM ·ln(Vfullscale / Vripple )·(Vfullscale / 16·Vripple )1/2
Referring again to the 8-bit case (illustrated graphically in Figure 1):
Given: RC = 4·TPWM
Tsettle = 22·TPWM = 0.69 ms
