圆波导双模滤波器的设计

    本周工作较忙，正式工作也有好多事情拖延，原本计划继续把移相器写完，但为了完成本周计划就写一篇自己熟悉的领域。
    前期写了一篇《如何设计带通滤波器》的文章，用的是梳线滤波器做的例子。我的初衷是想通过一个梳线滤波器的设计来介绍带通滤波器的通用设计过程，但中途有网友问滤波器/微带线滤波器如何设计，我想说所有结构的带通滤波器都可以按照之前文章的方法来操作，前提是需要积累各种结构滤波器的谐振器形式，能量耦合方式，很大程度上经验也是体现在对各种结构电学特性的理解上而不是掌握多少种设计方法上。今天讲解一个圆波导双模滤波器的设计，来更进一步体会带通滤波器的设计方法。
    圆波导双模滤波器Q值高，结构紧凑，可以高可靠的实现复杂的滤波器函数特性（无需探针或耦合环等结构），当采用殷钢材质时可以实现超高的温度稳定性。所以广泛的应用在卫星系统中。
    1、圆波导双模滤波器的工作原理

    带通滤波器的工作原理时通过适当的能量交换结构（耦合）实现几个互不相关的谐振器（能量储存）间的能量传递，从而实现滤波功能。圆波导工作的主模是TE11模，由于圆波导的对称性，当利用圆波导作为谐振器时，在一个圆波导的腔体内包含两个相互正交（无能量交换）的极化简并模如图 1所示，这就类似于两个无能量交换的同频率谐振器，这样就可以用一节谐振器的体积实现两个谐振器的功能，从而可以减小波导滤波器的体积。

    图1 圆波导中两个相互正交的简并模

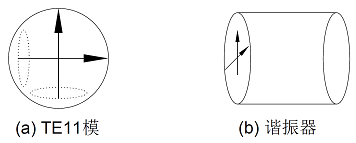
    一个双模带通滤波器的工作原理见图 2所示，一个矩形波导馈入一个垂直极化的电场。

    图2 双模带通滤波器的工作原理
    进入圆波导谐振器后，激起模式1的垂直极化场，通过一个45°的螺钉使垂直极化场产生了水平极化分量，激励起模式2的水平极化场，从而实现了垂直极化场和水平极化场的耦合。模式2的水平极化能量可以通过一个垂直的M23耦合小窗实现两个圆波导谐振器间水平极化场的耦合，依次类推便实现了能量在波导管中的储存传递，实现滤波。
    2、圆波导双模滤波器的设计步骤
    波导滤波器的设计步骤和《如何设计一个带通滤波器》里的梳线滤波器设计步骤基本一样，这里对设计过程就尽量简化。
    设计过程如下：
    1) 本征模式确定谐振器尺寸
    2) 输入耦合窗尺寸确定
    3) 12两个极化简并模式间的耦合螺钉深度计算（34和12对称）
    4) 23两个波导腔间耦合窗口计算
    5) 滤波器整体仿真
    本征模式确定谐振器尺寸

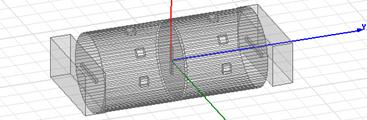
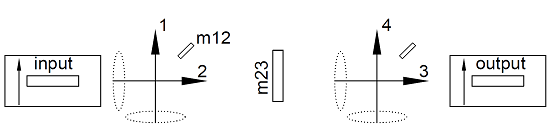
    建立图 3所示的圆波导本征模式仿真模型，确定谐振在11.5GHz的TE11模式圆波导尺寸，由于圆波导中模式复杂，可以通过场型观察确认模式选择是否正确。通过仿真，谐振器尺寸大概为半径R=9.5mm，长度L=22.3mm。

    图3 本征模式确定谐振器尺寸
    输入耦合窗尺寸确定

    通过excel时延计算工具（前期分享）得到，该滤波器的输入时延需要4.8ns,在HFSS中建立图图 4的模型，通过计算可以的得到耦合窗口的尺寸为LM01=11.5mm。谐振器由于耦合窗的作用尺寸偏长，可适当缩短至22mm。

    图4 输入耦合窗口计算
    12两个极化简并模式间的耦合螺钉深度计算（34和12对称）

    12间极化简并模式的耦合是通过两个模式间一颗45°的螺钉实现的，时延需要7.8ns，在HFSS中建立图 5所示的模型，通过仿真，找出M12耦合螺钉的长度M12=1.6mm。（小技巧：双谐振器仿真时先任意指定一个耦合值，稍微大一些。先调谐2谐振器的频率，将时延谐振峰值找对称，之后在确定耦合尺寸。）

    图5 M12耦合螺钉尺寸确定
    23两个波导腔间耦合窗口计算

    23耦合属于两个波导腔中同极化模式的耦合，群时延大小需要14ns，可以用图 6所示的模型来确定23耦合窗口的大小，经过计算M23=8.3mm。

    图6 窗口耦合尺寸确认模型
    滤波器整体仿真

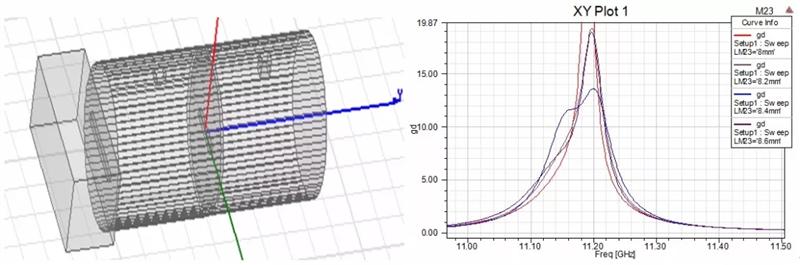
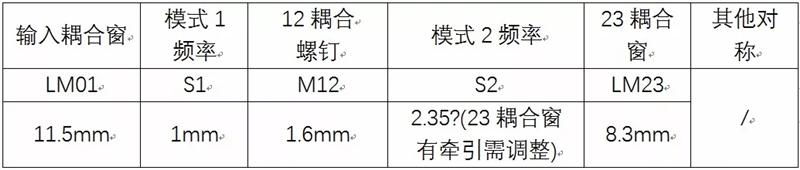
    经过上述步骤的仿真后关键尺寸确定如表 1所示。在HFSS中建立完整的双模滤波器仿真模型，大部分的尺寸都由前面几步的仿真确定了，但模式2的频率由于23窗口耦合因素没有考虑，螺钉深度不确定，现阶段S2深度是影响滤波器性能的关键参数。

    表1 双模滤波器关键尺寸表
    修正S2的方法有很多，这里由于模型较简单可以通过扫描方式直接准确找出S2的深度，经过扫描可以发现S2深度在2.3mm时双模滤波器性能已经很不错了见图 7所示。如果追求完美可以通过调谐，优化，或者参考之前的《参数提取法设计带通滤波器》对滤波器性能进行调谐。实际上由于腔体滤波器的调谐范围非常大，到这个阶段后就没有必要仿真了。

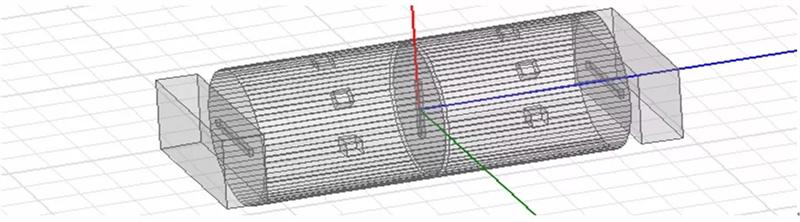
    通过结果可以看到，我们通过两节波导腔实现了4阶的滤波器。如果感兴趣可以适当修改下腔体里的简并模耦合螺钉位置，把腔体间的窗口改成十字槽，可以发现这种滤波器很容易实现CQ式的广义切比雪夫滤波器。文章中为了节省时间仿真时采用了很多近似，仿真时可能存在误差，但不影响对双模滤波器设计方法的了解。

    图7 双模滤波器模型及性能