一种异质多传感器的异步量测融合算法验证

在多传感器目标跟踪系统中，由于异质传感器能实现优势互补，将其数据进行融合，可提高对空中目标的跟踪。异质传感器信息融合是数据融合实际应用中的一个重要内容，因为在实际的系统中，经常遇到利用3D雷达（测量值为距离、方位和俯仰）、2D雷达（距离和方位）、被动雷达（方位和俯仰）、测高雷达（俯仰）和ESM（方位）等传感器对目标进行跟踪，利用这些传感器进行融合可获得更、更完全的目标状态估计。
　　异质多传感器融合是数据融合中一个重要内容，文献［1］研究了利用2D主动雷达和红外传感器对高机动目标进行跟踪，提出基于IMM／PDAF的序贯滤波融合方法。文献［2-4］提出一种虚拟融合法，由于该算法首先是对采样率高的传感器数据进行二乘压缩，使之与另一个传感器的数据同步，该算法中各传感器采样率的比需满足一定的条件，文献［5］研究了一种并行滤波方法。由于该算法是一种同步融合算法，对于异步数据首先要进行同步化。
　　本文从建立伪量测方程的角度，提出了一种异质多传感器的异步量测融合算法，该算法是通过在融合中心建立伪量测方程使各传感器的数据同步，然后利用同步的思想进行处理，通过计算机仿真进行了验证。
　　2 系统模型
　　不失一般性，以在球面坐标系中运动的目标为例进行分析，则离散时间线性系统的状态方程为：
　　X（k+1）=F（k+1，k）X（k）+Γ（k+1，k）V（k） （1）
　　其中，X（k）为k时刻目标的状态向量；kF（k+1，k）为状态转移矩阵；Γ（k+1，k）为过程噪声转移矩阵；V（k）是零均值，高斯白噪声序列，其协方差阵为Q（k）。
　　在实际情况下，传感器得到的是三维球坐标系或二维极坐标系的目标量测，即包括斜距r、方位角a和俯仰角e。假设某一传感器的测量方程为：
　　Z（k）=h（X（k））+W（k） （2）
　　其中，W（k）是k时刻的测量高斯白噪声，其相互独立且协方差为R（k），量测向量Z（k）包括斜距r（k）、方位角a（k）、俯仰角e（k），坐标转换如图2所示，由其定义可得：
　　

　　3 测量方程的线性化
　　由于测量方程（2）是一个非线性方程，可以利用泰勒级数展开，对其进行线性化，展开围绕者预测状态X（k／k-1）进行，表示如下：
　

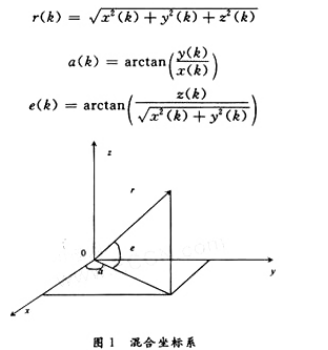
　　其中观测斜距用的量测矩阵Hr（k）由下式表示为：

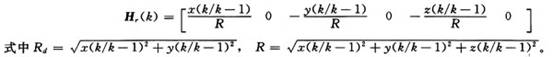
　　故状态方程（1）和测量方程（4）组成线性化目标运动模型。
　　4 融合算法
　　假设采用N个传感器对目标进行观测，Ti是第i个传感器的采样间隔，且在每个时间间隔［（k-1）T，kT］（T为融合周期）内各传感器共产生了Nk个量测，在该时间间隔内，某个传感器可能产生一个或几个量测，nik为传感器i提供量测的数目，则有：

　　若某个传感器j，在该时间间隔内没有提供量测，那么在式（5）中nik=0，这些量测在该时间间隔内是任意分布的。
　　令λik（i=1，2，…，Nk）为获得第i量测时间与KT之间的间隔，为方便标记，以下KT简写为K，如图2所示，则量测i的测量方程可表示为：

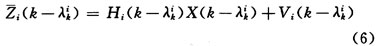
　　则单个融合间隔内的量测集合可表示为：

　　直到k时刻为止各传感器所有量测集合可表示为：

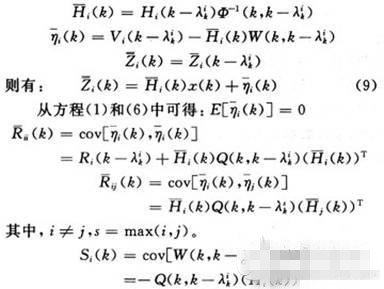
　　其中，Z（k），H（k），η（k）分别为扩维后的观测矢量、观测矩阵和测量噪声矢量，且有E［η（k）］=0，伪量测噪声之间的协方差矩阵为：

　　伪量测噪声与系统噪声之间的协方差矩阵为：

　　在条件1下，根据伪系统模型（1），（10），通过求解给定伪测量条件下关于目标状态的概率密度函数推导出相应的并行滤波异步数据融合算法：

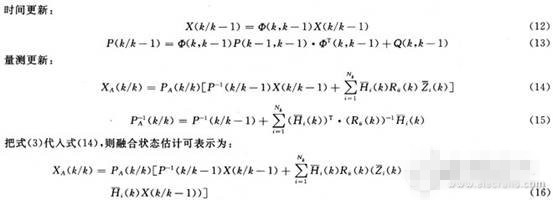
　　则式（12）～（16）构成了异质多传感器扩维滤波融合算法，从中可知，该异步数据融合算法，计算较为简便，但其是在条件1下的滤波融合，故该算法在性能上为次优。
　　5仿真分析
　　假设采用雷达（测量值为斜距，方位角和俯仰角）和红外（方位角和俯仰角）2个传感器同时跟踪1个目标，设匀速直线运动目标的初始状态向量为x（0）=［30 000，-200，20 000，150，1 000，10］T，测量周期为T1=T2=2 s，传感器2比传感器1晚1 s开始采样，雷达和红外传感器的测距、测方位和测俯仰的为：σr=100 m，σa1=7 mrad，σa2=6 mrad，σe1=2 mrad，σe2=1 mrad，进行100次Monter Carlo仿真实验，采用滤波RMSE的均值Ps来度量各融合算法的估计，且：

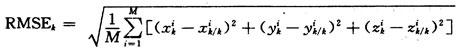
　　仿真结果如图3所示。

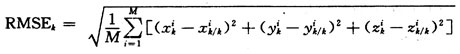
　　6结语
　　本文提出一种不同传感器数据的融合算法，即首先是通过建立伪量测方程得到同步化的伪量测数据，之后利用一种扩维滤波的思想得到目标状态的估计，由于该算法适用与不同类型传感器异步数据的融合，所以该算法是一种实际算法。从本文提出算法的仿真结果可以看出，目标3个方向位置和速度融合均方误差均能得到较好的效果，且本文提出的算法是一种并行处理的思想，所以数据处理的速度高，特别适用于异步数据的融合处理。