在无线通信系统中,日益增加的语音和数据信息必须在一个固定带宽中传输,无源互调失真已经成为限制系统容量的重要因素。就好像在有源器件中,当两个频率以上的信号以一个非线性形式混合在一起时,就会产生一些伪信号,这就是无源互调信号。当这些伪互调信号落在基站的接收(上行)频段内时,接收机就会发生减敏现象。这种现象可以降低通话质量,或者降低系统的载干比(C/I),从而减少通信系统的容量。
造成无源互调的原因很多,其中包括机械接触不良,射频通道中的含铁导体,和射频导体表面的污染。事实上,很难准确预知器件的无源互调值,测量所得的数据只能用来大致描述器件的性能。由于结构技术方面的微小改变都会导致互调指标的严重变化,所以一些生产厂商通过对产品100%的检验来保证基站中使用的射频器件的无源互调水平都能满足指标要求。
当存在两个或两个以上频率时,基站的大功率传输通道中的每个组件和子系统都会产生互调失真。本文仅关注其中的一种组件:集成电缆。针对集成电缆产生的互调失真既是有方向性的,又是依赖于频率的理解,对于集成电缆的指标及其在通信基站中的使用是一个非常重要的因素。
一条集成电缆(或者是任何两端口射频器件)都有两种无源互调响应:反射互调和通过互调。图1为Summitek公司的无源互调分析仪测量这两个互调信号的原理。在SI-1900A型设备中,通过端口1向集成电缆注入两个大功率信号,电缆的另一端与端口2连接。端口2作为这两个大功率信号的负载,并且其无源反射互调很小,可忽略。在端口1处测量反射无源互调响应,在端口2处测量通过(即前向)无源互调。与目前使用的大多数无源互调测试设备不同的是,Summitek公司的互调分析仪支持前向和反向互调响应的同时测量,而不需要重新接驳。这样可以避免重新接驳时所必须的配对和再配对操作,从而使反射响应和通过响应的测量误差化。将该特性与Summitek分析仪的扫频互调测量功能相结合,就可以对电缆完整的互调特性做测量了。
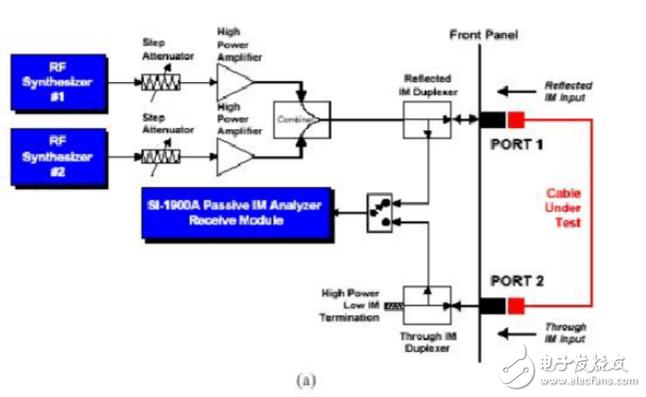

图2中的模型有助于对集成电缆的反射和通过互调特性的理解。
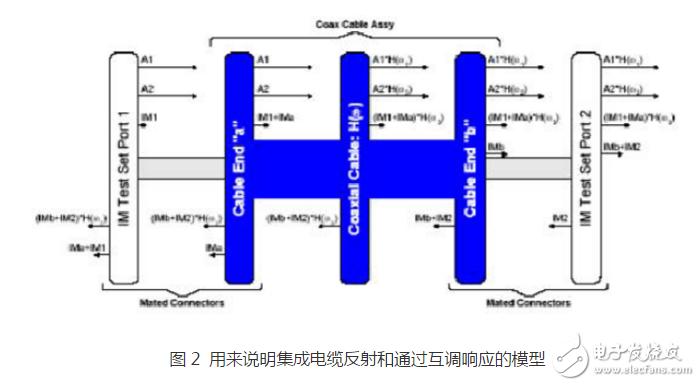
图中的中间部分是集成电缆本身。在这个模型中,关键是假定集成电缆中只有接头部分产生互调。换句话说,尽管当信号沿着电缆的长度传输,电缆本身会产生损耗和群时延,但是相对于接头,电缆本身不产生大的互调,可以用图2中H( )的传输函数来表示。用IMa和IMb来表示集成电缆接头产生的互调响应。在本模型中,我们假设互调只产生在每个接头中单一的一点上,并且假设互调一旦产生后,其双向传输是等能量传输的。
模型的左边是端口1,该端口用来将两个+43dBm的信号注入集成电缆(见图1(a)的框图)。这两个信号在图2中表示为向量A1和A2。无源互调测试系统本身也会产生互调,用向量IM1表示。注意,和该模型中的其他互调响应一样,IM1响应也是自其产生处双向传输的。假定,端口1的互调响应和电缆a端的互调是协同定位的,换句话说,这两个互调源之间的电磁波距离可以忽略不计。
模型的右边是端口2,该端口也会产生一个不希望出现的小互调能量,以IM2表示。所有用于端口1的假设同样适用于端口2。通观完整的集成电缆无源互调的测量模型,以下几条值得关注:
每个测试端口都有与其相关的4个互调响应。其中两个是接头末端产生的,另两个是互调分析仪自身产物。
电缆b端的互调(IMb)和端口2的互调(IM2)会通过电缆反向传输,从而产生的反射互调响应可以在端口1处测量。
电缆a端的互调(IMa)和端口1的互调(IM1)会通过电缆进行传输,从而产生的通过互调响应可以在端口2处测量。
通过这个模型,集成电缆的互调值就可以被确定了。
虽然预计一个给定的射频器件的互调是非常困难的,但是单个互调源之间的相互作用在图2的模型中可以很容易地被表现出来。
首先,我们已经知道了每一个互调源的三阶互调公式。以端口1和电缆a端的响应开始,互调响应为:
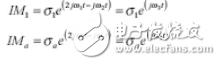
三阶互调的频率为:
w3 ≡2ω2 ?ω1
t:时间
IM1:端口1的三阶互调响应
IMa:电缆a端的三阶互调响应
σ1:端口1的互调系数,即端口1(=10[dBc/20.])的dBc响应的简单数字转化
σa:端口a的互调系数,即端口a(=10[dBc/20.])的dBc响应的简单数字转化
ω1, 2, 3:分别为载波1,载波2和产生的三阶互调响应的频率弧度
电缆b端和端口2的互调响应相对稍微复杂。两个载波产生的互调响应可以通过电缆传输函数H(w)表示。为了简化公式,和消除非线性功率对互调产物及其载波的影响,假设电缆是无损耗的。在公式中,这个假设表示为:
|H(w) |= 1
当终结果出来时,这个假设对于模型度的影响是非常显著的。
即使假设电缆是无损耗的,电缆产生的群时延还是被包含在模型中的,具体如下式:
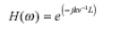
其中:
k:与频率有关的通过电缆(2p/l)的电磁波数
v:同轴电缆的传输速率
L:电缆的长度
电缆b端和端口2的互调响应表示为:
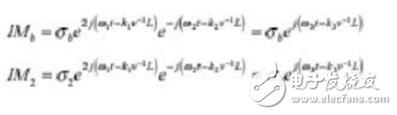
当公式中IMa、IM1、IMb、和IM2已知,落在端口2上,总的通过(前向)互调表达式为:
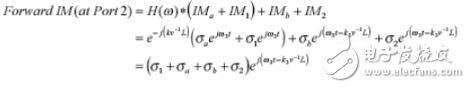
上式表示同时落在互调测试设备端口2上的四个互调响应,不依赖于互调频率。假设单独的互调源是不依赖于频率的,且电缆的损耗是一个常数,那么整条集成电缆的通过互调响应将不依赖于频率。
我们可以采用相似的过程来描述反射互调响应。反射互调响应可以由下式来给出:
Reflected IM at Port ( 1) = IMa + IM1 + H(w)?(IMb + IM2 )
简化为:
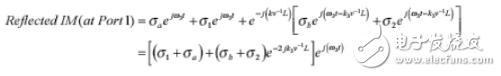
上式表示端口1中的反射互调响应是端口1和电缆b端响应的合成,加上由于电缆b端和端口2的互调响应的合成造成的移相响应。由于存在一个不同相位的互调源的合成向量,所以,我们认为反射互调响应是一个与电缆的频率和电长度有关的函数。
为了验证该模型,我们使用SI-1900A型无源互调失真分析仪来测量无线通信应用中一种典型的集成跳线。该集成跳线长1.5米,厂商标注的速率因子为82%,两端分别安装有一个DIN-M型接头。载波功率设置为20W/路。分析仪的自适应逻辑电路确保了测试过程中,载波的功率变化不超过0.2dB。分析仪的底噪不超过-140dBm,即当施加一个+43dBm的载波功率时,分析仪的互调底噪不超过-163dBc。
图3显示了反射和通过互调响应的测量结果曲线,以及相应的预测曲线。电缆每个端口上的互调响应值,是通过假设前向互调响应是由两个分别在电缆两端的等幅互调源之和组成的。反射互调响应值仅由该模型来决定,且不用调节使之与测得的数据相匹配。

如图3所示,尽管预计数据中的反射互调响应0点的深度值远远大于实际测得的数据,但是总的通过和反射响应趋势是符合模型的预计曲线趋势。这非常可能是由于模型中的简单假设和电缆实际性能之间的差别造成的。
1)假设在模型中的互调源是等幅的。但是实际上,电缆两端的互调响应可能并不是等幅的。这就导致了模型的互调0点值好于测量所得数据。
2)在这个简单的模型中,假设电缆是无损耗的,那么,当互调从电缆的一端传输到另一端时,将仍然维持原始的振幅。但是实际测量中,互调从电缆的一端传输到另一端时,必将产生损耗,这就会造成电缆中两个互调响应的不一致,从而产生一个深度较浅的0点值。
3)假设测试设备所产生的互调响应与电缆接头的互调响应是协同定位的。在实际测量中,由于在测试设备的端口1和端口2上使用了接头保护器(插孔适配器),使得测试设备和电缆接头之间产生3cm的距离,进而大约在测得的0值深度处产生额外的互调响应。
在简化的无源互调模型中,电缆的反射互调和通过互调被准确的预计。而且模型预计和实际测量所得的结果之间的差异也可以很容易解释。
负责系统的整体实现和器件的互调性能的工程师可以通过这些结果的应用,来帮助理解现场或实验室环境中的无源互调测量。基于以上结果的结论包括:
如果电缆是低损耗的,且电缆每一端产生的互调被认为是基本相似的,那么一般来说,测得的通过互调响应比电缆任一端的响应大6dB,而且通常与频率无关。该响应表现为电缆反射或通过互调测量中的(或接近)的互调响应。
如果测量低损耗电缆的反射无源互调,那么测得的互调值会随着互调频率的改变而改变。因此,测量单一频率的反射互调可能不能真正说明整个系统产生的无源互调失真的影响。
合理选择电缆的长度可以导致互调源之间的相消干扰,从而产生一个低的系统互调响应。这个特性可以用来选定发射机架与基站调谐箱面板间跳线的长度,实现频组分配。
当长电缆的一端产生的大互调响应与电缆另一端的小互调响应合成时,很可能会产生一个与频率高度相关的反射互调响应。这种情况可能是因为基站中有一个由于有缺陷或设计不合理的天线返回的大互调信号造成的。
当同轴电缆的温度改变(比如,电缆的损耗发热或者阳光的照射)时,电缆的电长度将会发生变化。这种变化会造成电缆长度的增加,以及速率因子的减小。当电缆的长度变化时,使得多个互调源间的相位改变,从而造成基站双工机接收端产生的互调值发生变化。那么,互调值随温度函数增加或减小,将会导致基站容量的变化。
虽然,本文以射频集成电缆为例来说明互调的测量,但该结论可以延伸并同样适用于任何两端口器件。根据器件本身传输函数的定义,与双工器、滤波器或天线相关的互调特性也可以被确定了。
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。