埋嵌式元件共面度测量方法研究（二）

　　4 测量方法改良

　　4.1 改良思路

　　对比共面度定义以及PCBA贴装和焊接过程对器件引脚共面度值的测量方法，结合公司前期共面度测量、分析经验，公司现有的埋嵌铜块共面度的测量方法有如下待改进之处（表7）。

　　

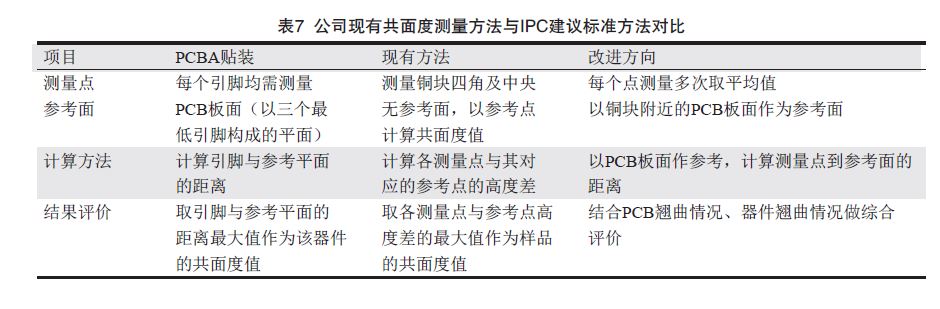
　　4.2 改良方法

　　从表7的分析可知，使用三维坐标仪测量公司埋嵌铜块的共面度，需要在参考平面选取、测量数据量、计算方法和结果评价方法方面进行优化，以使其更加符合共面度原始定义，测量结果更能与客户需求呼应。

　　4.2.1 参考平面选取

　　根据共面度定义，被测点的共面度值反映该点与基准面之间的偏移量，对于PCB上的埋嵌铜块而言，其基准面应是铜块所在的PCB局部区域，而非整个PCB板面。而为便于区分埋嵌铜块不同位置的共面度值，我们仍测量器件的四角与中央共五个点，同时测量PCB板面对应铜块四角位置的四个点（板面上点与铜块的距离一般为0.5 mm ~ 1.0 mm），铜块对应的基准面由PCB板面的这四个点构造。

　　三维坐标仪输出的各点测量结果是三个数字一组的数据（如（5.012,10.251,-0.026）），分别代表测量点所在的X、Y、Z坐标，这一个个点在一个三维空间内。

　　在高等数学内有如下定义和定理：

　　定理一：空间内任意两个点之间的连线，以及其连接方向，可以确定一个向量；

　　定理二：不在同一直线上的三个点，可以确定一个平面；

　　定理三：过一点做点外一个平面的垂线，则点与垂足组成的线段的长度即为该点到平面的距离。

　　基于上述定义和定理，我们可以把PCB板面的各测量点组成向量，并构造出平面，然后计算铜块表面各测量点到平面的距离，就可以得到测量点的共面度值。

　　测量PCB板面呈方形的四个点A1、B1、C1、D1,对于每个测量点，选取与其直角相邻的2个点构造一个平面，则可构造四个平面，如图9所示。定义A1、B1、C1、D1对应的平面为α1、α2、α3、α4.

　　

　　下文以构造点A1、B1、D1对应的平面α1为例，介绍使用PCB板面测量点的坐标、采用点法式方法构造基准平面的过程：

　　（1）选取构造点：设A1点坐标为（x1,y1,z1），B1点坐标为（x2,y2,z2），D1点坐标为（x4,y4,z4）；

　　（2）构造向量：向量A1D1记为a1{（x4-x1），（y4-y1），（z4-z1）},向量A1B1记为b1{（x2-x1），（y2-y1），（z2z1）};

　　（3）计算平面法向量：

　　

　　（4）构造平面α1:点法式方程为：

　　

　　同理可利用A1、B1、C1点构造B1点对应的基准平面α2,B1、C1、D1点构造C1点对应的基准平面α3,C1、D1、A1点构造D1点对应的基准平面α4.

　　4.2.2 测量数据量

　　为兼顾测量效率和测量结果准确性，设计每个点测量1、2、3次的计算方法，其中每个点测量2、3次时，每次测量时需对同一位置测量2、3次，计算共面度时各点坐标取测量的平均值。

　　计算共面度时的优先顺序为：单点3次>单点2次>单点1次。可在优先（Excel）表格内编程，实现数据优先级设定。

　　4.2.3 共面度值计算

　　如图10,计算铜块表面A（xA,yA,zA）点到基准面的共面度，基准面为点A1、B1、D1所构造的平面α1,已知A1点坐标为（x1,y1,z1），平面α1的点法式方程为：

　　

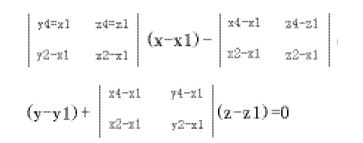
　　则A（xA,yA,zA）点到其基准平面α1的距离dA可用下式计算：

　　

　　同理，可计算铜块表面其它各点B、C、D距离其对应的基准平面的距离dB、dC、dD.对于铜块表面中央点E,由于其距离PCB表面参考点A1、B1、C1、D1均较远，故分别计算其到α1、α2、α3、α4四个基准平面的距离dE1、dE2、dE3、dE4,并考量四个计算值的差异，用以辅助评价被测PCB样品是否存在翘曲、样品在测量台面上是否被水平放置。

　　上述铜块上各点到基准平面的距离dA、dB、dC、dD、dE1、dE2、dE3、dE4,即为被测铜块表面各点的共面度值。dA、dB、dC、dD、dE1、dE2、dE3、dE4中者，即为被测铜块的共面度值。

　　4.2.3 结果评价

　　（1）各点共面度值：A、B、C、D点共面度值为dA、dB、dC、dD,E点共面度值为dE1、dE2、dE3、dE4中者；

　　（2）铜块共面度值：dA、dB、dC、dD、dE1、dE2、dE3、dE4中者；

　　（3）测量结果有效性判定：

　　①被测PCB板应被水平放置在测量台面上：若被测PCB板上直角相邻的两个基准点之间的高度差与其直线距离的比值>0,则视为被测PCB板可能存在斜放，需调整后重新测量。如：

　　（z2-z1）/（y2-y1）>0.5%或（z4-z1）/（x4-x1）>n‰，则被测PCB板可能存在斜放。

　　②被测PCB板在埋嵌铜块区域内存在翘曲：若被测PCB板上某个基准点距其对角的基准点所对应的基准面的距离与该两点直线距离的比值>0,则视为被测PCB板在埋嵌铜块区域内可能存在翘曲，需更换PCB或铜块样品重新测量。

　　③被测埋嵌铜块存在翘曲：若被测埋嵌铜块上各测量点共面度值极差与该铜块上对角线两点直线距离的比值>0,则视为被测埋嵌铜块可能存在翘曲，需更换PCB或铜块样品重新测量。

　　4.2.4 标准化和程序化

　　对使用公司三维坐标仪测量埋嵌铜块共面度的测量方法进行规范，如镜头放大倍率设定、聚焦取景范围设定、光源类型和亮度设定等。

　　对于测量结果的计算和评价，设计专用表格和程序，处理数据时只需将原始数据（。txt格式）转化成电子表格格式（。txt格式）后粘贴到指定表格内，即可显示测量结果和评价结果。

　　4.3 改良效果评价

　　4.3.1 改良前后的测量结果对比

　　使用公司三维坐标仪，分别采用直接比较五点法和改良后的五点法测量同一嵌铜块样品的共面度，对比测量结果如表8、表9.

　　

　　

　　由上述数据可见，采用改良后的五点法测量结果极差减小，平整度值相对较小，原因是采用构造平面的方法减小了直接对比法计算共面度值带来的误差。

　　4.3.2 重复性和再现性评价

　　使用公司三维坐标仪、5个嵌入铜块样品、分别由3个不同测量人各随机测量3次，对测量结果做重复性和再现性评价如表10、表11.

　　

　　

　　由上述分析可见：

　　（1）使用三维坐标仪测量铜块样品的共面度，重复性变差0.006 mm,再现性变差0.004 mm,重复性和再现性变差0.009 mm,占样品公差范围（±0.152 mm）的6.03%,说明该方法的重复性和再现性很好；

　　（2）五个被测铜块样品的共面度σ为0.003 mm、样品变差 （PV）为0.015 mm、占铜块样品共面度公差范围（±0.152 mm）的9.73%,说明被测铜块样品表面平整，公司埋嵌铜块产品共面度良好。

　　4.4 测量方法标准化和程序化

　　针对该新开发的埋嵌铜块共面度测量方法的测量操作（样品放置、光源选择、镜头放大倍率设定）、数据记录、结果分析等要求，建立一套共面度测量操作和测量结果计算的规范。且针对埋嵌铜块共面度测量结果的原始数据处理、基准平面构造、各测量点共面度值计算过程均已在EXCEL表格内完成编程，形成埋嵌铜块共面度测量数据处理专用软件。使用人员只需将三坐标仪测得的原始测量数据（。txt格式）转化成电子表格（。xls）格式，再复制、粘贴到指定的表格区域内，即可显示共面度值计算结果和测量结果有效性判定结果。其余非操作界面和后台计算界面均已加密处理，避免操作人员误操作损害软件。

　　5 总结

　　通过对电子行业内有关共面度的定义、共面度的测量方法和相关标准的了解和吸收，在公司原有较简单的埋入/嵌入铜块共面度测量方法（切片观察法、直接比较五点法）基础上，开发了一种新的埋入/嵌入铜块共面度测量方法及其软件，该方法具有如下特点：

　　（1）可对埋入/嵌入铜块样品进行无损、重复、高在线测量，测量结果可智能计算，且包含测量结果有效性判定功能；

　　（2）利用高等数学方法对大量原始测量数据进行有效处理，从而得到准确的埋嵌铜块共面度测量结果；

　　（3）将原始数据处理过程、共面度值计算过程、共面度计算即时显示功能以及计算结果有效性判定等功能实现程序化和模块化，减少了埋嵌铜块共面度测量的工作量和出错概率，提高了该测量方法的实用性；

　　（4）相比电子行业常规测量方法，不需新增专用设备，节省了设备投资或改造费用。

　　科技、社会的发展推动着PCB行业的迅猛发展，在赋予我们无数机遇的同时也带给我们前所未有的挑战，它将永远鞭策着我们不畏艰险、迎难而上。在开创PCB新工艺、新技术、新产品的道路上，我们任重而道远。

　　开启新思维、提出新见解、采用新方法，不断开发出符合客户要求的高科技产品将是我们永远的追求和动力。