基于FilterPro 和Proteus 的带通滤波器设计

　　摘要：传统的带通滤波器设计方法中涉及了很多复杂的理论分析和计算.针对上述缺点，介绍一种使用EDA软件进行带通滤波器的设计方案，详细阐述了使用FilterPro软件进行有源带通滤波器电路的设计步骤，然后给出了在Proteus中对所设计的滤波器进行仿真分析和测试的方法.测试结果表明，使用该方法设计的带通滤波器具有性能稳定.设计难度小等优点，也为滤波器的设计提供了一个新的思路.

　　0 引言

　　带通滤波器是一种仅允许特定频率通过，同时对其余频率的信号进行有效抑制的电路.由于它对信号具有选择性，故而被广泛地应用现在电子设计中.但是，带通滤波器的种类繁多，各个类型的设计差异也很大，这就导致了在传统滤波器的设计方法中不可避免地要进行大量的理论计算与分析，不但损失了宝贵的时间，同时也提升了电路的设计门槛.为了解决上述弊端，本文介绍了一种使用FilterPro和Proteus相结合的有源带通滤波器的设计方案，随着EDA技术的不断发展，这种方法的优势也将越来越明显.

　　1 带通滤波器设计工具简介

　　1.1 滤波器设计软件FilterPro

　　FilterPro 是美国TI（德州仪器）公司推出的一款的滤波器设计软件，它支持低通.高通.带通以及全通滤波器的设计，同时也支持常见的贝塞尔.巴特沃斯以及切比雪夫响应类型.设计人员只需要根据滤波器的设计向导按部就班地往下进行，就可以得到符合要求的滤波器电路，同时还可以得到与之相对应的响应曲线.

　　但是有一点需要注意：这款软件的计算结果是一个连续域的计算结果，只有当使用的运算放大器是理想的运放时才能得到与所给响应曲线完全吻合的响应结果，但这并不影响我们使用它进行滤波器的设计.因此只需要使用其他基于Spice 模型的EDA 仿真软件对电路进行仿真分析和调整，这就可以设计出性能稳定的滤波器电路.

　　1.2 电路仿真软件Proteus

　　Proteus 软件是英国Labcenter electronics 公司开发的一款功能强大的EDA 软件，它自身集成了丰富的元件库，更具有其他软件无法与之相媲美的单片机仿真功能，使得它被广大单片机设计人员所熟知.其实Prote-us在模拟电子的设计与仿真中做的同样出色，只不过对它在这方面的介绍较少.

　　Proteus中独特的图表分析法可以实现多种类型的仿真.本文所设计的这款带通滤波器就是在Proteus使用频响曲线图表进行分析的.

　　2 有源带通滤波器的设计

　　在实际电路设计中需要构造一个中心频率40 kHz.通带10 kHz的二阶带通滤波器来获取有用的信号.常用的二阶带通滤波器有多反馈型和Sallen-Key型，二者在电路的设计上略有区别.由于多反馈型带通滤波器的品质因数Q.中心频率f 以及增益A 都可以独立调节，所以终决定使用多反馈型的带通滤波器.为了使通带内的信号尽可能平滑，在此使用了响应类型为巴特沃斯型的带通滤波器.下面将介绍如何使用FilterPro 进行带通滤波器的设计：

　　（1）打开FilterPro 的设计向导并选择滤波器的类型，此处选择带通滤波器（即“BandPass”），点击“Next”;

　　（2）设置滤波器的具体参数，这是关键的一步.根据上面的分析，以此设置中心频率.通带带宽以及滤波器的阶数，把增益设为2（大约6 dB），设置的结果如图1所示，然后点击“Next”;

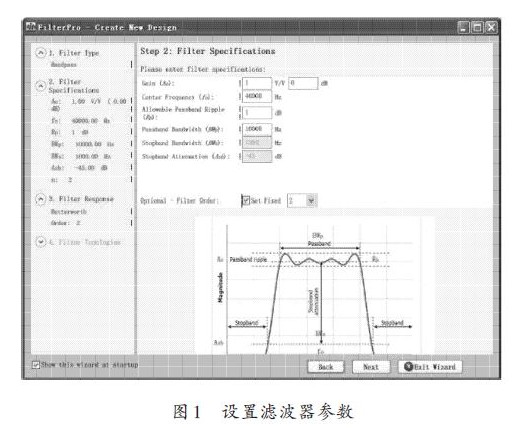
　　（3）接下来选择滤波器的响应类型，在这里选择巴特沃斯类型，点击下一步；

　　（4）在滤波器的结构类型里面我们选择多反馈型，点击“完成”.

　　通过上面的四个步骤，带通滤波器电路就自动生成了，终的电路原理图如图2所示.然后可在Proteus中搭建电路进行仿真分析，前面已经提到，FilterPro生成的滤波器中的运放使用的理想运放模型，所以仿真时需要先用理想运放进行分析，然后再进行替换.

　　3 滤波器的仿真与测试

　　下面使用Proteus中的图表分析法来分析图2所示的滤波器.首先，在Proteus工作区中搭建图2所示的电路.其中运放使用理想运放，然后使用Frequency来分析滤波器的频响特性曲线，其具体方法如下：在Proteus的设计空间的空白处单击右键，依次选择“Place→Graphs→Frequency”,此时鼠标就会变成铅笔状，拖动鼠标即可画出一张Frequency 表，然后将OUTPUT 探针分别拖到Frequency图标的左上角和右下角，此时你会看到左上角会显示ONPUT和Gain（dB），而右下角会显示OUTPUT和phase（即相位），终设计好的Frequency图表如图3所示，然后设置参考信号源，这里即图2中的输入信号INPUT,设置如图4所示.

　　现在即可以进行仿真分析，依次点击图3 中的“Graph→Simulate Graph”即可获得频响曲线，如图5所示.

　　从Frequency图中可以看出，这个带通滤波器的中心频率为40 kHz（图表底部中间的FREQ），增益为5.91 dB（图中右下角OUTPUT）这与理论值6 dB 很接近，说明从理论上来讲这个滤波器电路是正确的.下面可以根据实际情况来搭建上述滤波器电路.在此使用LM324来搭建该滤波器电路，由于使用单电源供电，所以LM324的正输入端需要加上偏执电压以确保信号的完整性，此外，由于滤波器在整个系统中处于中间部分，所以输入和输出端都需要加入隔直电容.终设计的滤波器电路如图6所示，其频响曲线如图7所示.

　　下面就进行信号的输入/输出测试.在此使用Pro-teus 的Analog 图表进行此项分析.在INPUT 端分别输入100 mV,40 kHz和100 mV,10 kHz的正弦信号，并观察输出，其结果如图8和图9所示.从图8和图9中可以看出，当输入信号的频率在通带以内时，信号都可以正常通过，而且具有一定的增益；当信号频率在通带外时，就会被滤波器抑制而产生较大的衰减.然后通过硬件电路调试也验证了上面仿真的正确性.

　　4 结语

　　本文介绍的这种带通滤波器的设计方法具有很强的通用性.实践表明，该方法不但可以避免一些复杂的理论计算和分析，同时通过仿真还可以直观的检验电路的输入和输出，进而使得滤波器的性能更加的稳定.另外，使用EDA 软件进行电路设计和仿真测试也可以有效地降低设计难度和设计成本，这种设计方法也为滤波器的设计提供了一种新的设计思路.