基于Matlab的FIR数字滤波器设计方案

　　摘要：目前，数字信号处理在通信、语音、图像、自动控制、雷达、军事、航空航天、医疗和家用电器等众多领域得到了广泛的应用。在数字信号处理应用中，FIR数字滤波器的重要地位日益突现并已获得广泛应用。

　　本文先介绍FIR数字滤波器的相关概念，并利用MATLAB中的FDA TOOL工具箱和Simulink工具进行FIR带通数字滤波器的设计，给出了基于Matlab的FIR数字滤波器设计方案。通过建模和仿真证明，本方案中设计的滤波器能够快速有效组成的常规数字滤波器， 实现不同截止频率的FIR滤波器，极大地减轻了工作量，实用性较强。

　　0 引言

　　随着信息时代数字化、智能化和网络化的发展，数字信号处理已成为一门极其重要的学科和研究热点，并且数字滤波技术作为该领域的一个重要组成部分得到了日益广泛的重视。

　　相对于IIR数字滤波器，FIR滤波器以其线性相位的极大优势得到了更加长足的发展。数字滤波器可以用硬件或软件两种方式来实现，而后者的优点是可以通过改变滤波器参数去调整整体性能，而MATLAB所提供的信号处理工具箱具有强大的函数功能，它不仅可以用来设计数字滤波器，还可以使设计达到忧化，因此它成为了FIR数字滤波器设计的强有力的工具。

　　1.FIR数字滤波器

　　1.1 FIR滤波器的系统函数

　　FIR数字滤波器是一种非递归系统，其冲激响应h（n）是有限长序列，其系统函数的一般形式为：

　　

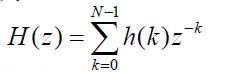
　　在上式中，h（n）是因果序列，H（z）是z1的N-1次多项式，仅在Z=0处有N-1阶极点，在其它地方没有极点，有N-1个零点处在有限Z平面内的任何位置上。FIR系统的基本结构有直接型和级联型，在雷达信号处理中作为相关器和对消器等获得了广泛的应用。

　　1.2 FIR滤波器的设计过程

　　数字滤波器的设计过程为：

　　1）按照实际需要，确定滤波器的性能要求。通常（但不总是）是在频域中给定数字滤波器的性能要求，一般为幅度和相位响应，即技术指标。

　　2）寻找满足预定性能要求的离散时间线性系统，即用一个因果稳定的系统函数去逼近给定的性能要求，以确定滤波器系数。

　　3）用有限的运算实现所设计的系统。

　　这里包括选择运算结构，对滤波器的系数、输入变量、中间变量和输出变量量化到固定字长。

　　4）通过模拟，分析其频率特性和相位特性，验证所设计的系统是否符合给定性能要求。

　　2.MATLAB相关工具介绍

　　2.1 FDATOOL工具箱

　　FDATOOL是Matlab软件中提供滤波器设计的专门工具箱，可以设计几乎所有的常规滤波器，其界面总共分两大部分，如图1所示。

　　

　　界面上半部分是特性区，用来显示滤波器的各种特性。

　　界面下半部分是Design Filter,用来设置滤波器的设计参数，主要分为：ResoponseType（滤波器类型）选项、Design Method（设计方法）选项、Filter Order（滤波器阶数）选项、Frenquency Specifications（频率特性）选项和Magnitude Specifications（幅度特性）选项。

　　2.2 Simulink简介

　　Simulink是一个进行动态系统建模、仿真和综合分析的集成软件包，它可以处理线性、非线性系统；离散系统、连续系统以及混合系统；单任务、多任务离散事件系统等，目前已经覆盖通信、控制、信号处理、电力系统等诸多领域。Simulink和Matlab的良好结合使得用户可以利用Matlab丰富的资源，建立仿真模型，监控仿真过程，并且可以在线修改参数，并观察改变后的结果。

　　3.FIR带通滤波器设计

　　针对含有5Hz、15Hz和30Hz的混合正弦波信号，设计一个FIR带通滤波器。参数要求：采样频率Fs=100Hz,通带下限截止频率Fc1=10Hz,通带上限截止频率Fc2=20Hz,过渡带宽6Hz,通阻带波动0.01,采用凯塞窗设计。

　　3.1 FDATOOL参数设定

　　Response Type中选择Bandpass;在DesignMethod选项中选择FIR Window,窗函数类型选取Kaiser,Beta值为3.4;指定Filter Order项中的Specify order为38;采样频率Fs=100Hz,截止频率Fc1=10Hz,Fc2=20Hz.设置完以后点击窗口下方的Design Filter,在窗口上方就会看到所设计滤波器的幅频响应，如图2所示。

　　

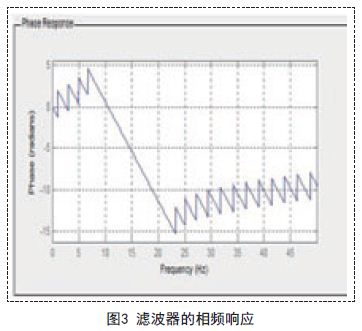
　　通过菜单选项Analysis还可以看到滤波器的相频响应（如图3所示）、组延迟、脉冲响应、阶跃响应、零极点配置等。设计完成后将结果保存为kaiser.fda文件。

　　

　　3.2 Simulink仿真

　　打开Simulink工具箱，新建一个Model,将正弦信号源和常量信号源、DSP离散正弦信号源、乘法器、加法器、示波器等布置好，并把各环节的端口按框图连接起来，搭建的系统仿真模型如图4所示，将上节中封装好的滤波器文件kaiser.fda导入Digital Filter Design模块，输入信号为：

　　

　　

　　生成的滤波效果如图5所示。

　　

　　图5中横坐标表示时间（t），纵坐标表示振幅。滤波后，信号周期约为0.067s,即频率为15Hz,通过对滤波前后的离散波形进行对比可以很明显的看出，复合信号通过设计的带通滤波器后，所需要的有用信号（15Hz）分离了出来，基本达到预期目的。

　　4.结论

　　本文提出的基于Matlab的FIR数字滤波器设计方案。先介绍FIR数字滤波器的相关概念，并利用MATLAB中的FDA TOOL工具箱和Simulink工具进行FIR带通数字滤波器的设计。

　　通过建模和仿真证明，本方案中设计的滤波器能够快速有效组成的常规数字滤波器， 实现不同截止频率的FIR滤波器，极大地减轻了工作量，实用性较强。（作者：白康）