单相全桥DC-AC电压逆变电路数字控制中的振荡现象分析

　　考虑数字控制采样计算延迟，建立了单相全桥DC-AC 电压型逆变电路在负载电压外环电感电流内环加给定电压前馈控制方法下的离散迭代模型。 通过分析相应的Jacobian 矩阵特征值轨迹，确定该数字控制逆变器失稳时分岔点类型为Hopf 分岔。 对离散迭代模型进行数学变换，得出了控制器边界的解析表达式以及系统发生分岔时振荡频率的解析表达式，从而揭示了系统发生振荡现象的内在物理机理。 ，通过Simulink 仿真以及电路实验证明了理论分析的正确性和有效性。

　　1. 引言

　　单相全桥DC-AC 电压型逆变电路在不间断电源（ UPS） 、分布式发电以及微型电网中有重要作用，得到了广泛应用。 同时，随着数字控制技术的不断发展成熟，特别是高性能数字信号处理器（ DSP） 的出现，使数字控制系统逐渐取代传统的模拟系统[1,2]. 数字控制下的电力电子逆变电路系统除逆变器自身的开关过程非线性外，还受到采样量化特别是采样、计算延时等问题的影响。 相对于模拟控制而言，数字控制电力电子逆变电路系统有更为复杂的非线性现象和工程应用背景。 研究数字控制电力电子逆变电路中的复杂非线性行为已经成为学术界的热点，具有重要的理论意义和工程应用价值。

　　已有学者对单相全桥逆变电路进行研究，取得了一些研究成果[3-9]. 文献[3-5]建立了工作在DC-DC 状态下的一阶H 桥式电路的离散映射模型，分析了其稳定性。 文献[6]对二阶H 桥式正弦逆变电路在比例积分（ PI） 单闭环模拟控制下快尺度和慢尺度的稳定性进行了研究。 文献[7]通过分析一阶H 桥式正弦逆变电路在比例（ P） 单闭环控制下的非线性行为，提出了慢变稳定性定理，分析了快变和慢变稳定性的关系。 文献[8,9]利用线性分析方法对一个开关周期延时数字控制下桥式逆变电路的工作特性进行了分析。 H 桥式电路工作在DC-AC状态下的情况较多，而单闭环控制单相全桥DC-AC逆变电路在实际工程应用中较少采用。 也有一些学者利用s 域模型和z 域模型对电力电子电路中出现的振荡现象进行了分析[10,11]. 然而，对于工程中常用的负载电压外环电感电流内环加给定电压前馈并且考虑一个开关周期延时的数字控制单相全桥DC-AC 电压逆变电路利用离散迭代模型对其非线性复杂行为的研究工作迄今未见报道。

　　本文以数字控制负载电压外环电感电流内环加给定电压前馈控制下的单相全桥DC-AC 电压逆变电路为研究对象，建立了其离散迭代模型，发现该逆变电路系统失稳时会发生Hopf 分岔。 通过对离散映射模型的进一步数学变换，得出了在不同负载情况下控制器参数稳定范围的解析表达式以及系统失稳后振荡频率的解析表达式，从而详细分析了单相全桥DC-AC 电压逆变电路系统的动力学行为和振荡频率与系统参数之间的关系，从而描述了系统的非线性行为，揭示了系统发生振荡的内在物理机理。 ，通过Simulink 仿真以及电路实验验证了理论分析的正确性。

　　2. 电路工作原理及数值仿真

　　2. 1. 单相全桥DC /AC 电压逆变电路数字控制原理

　　数字控制负载电压外环电感电流内环加给定电压前馈的单相全桥DC-AC 电压型逆变电路系统结构如图1 所示。 图中，E 为H 桥直流侧电压； S1-S4为理想电力电子开关； L,C 分别为滤波电感和滤波电容； R 为负载电阻； CM,VM 分别为电流传感器和电压传感器； IL,VR分别为电感电流和负载电阻电压的采样值，由于采样保持器的作用，采样结果在一个采样周期内恒定，呈阶梯状； VRref为输出电压参考值； ILref是外环控制器输出，将其作为电感电流内环的参考值； I*c是调节器输出的中间变量； Ic为控制信号。

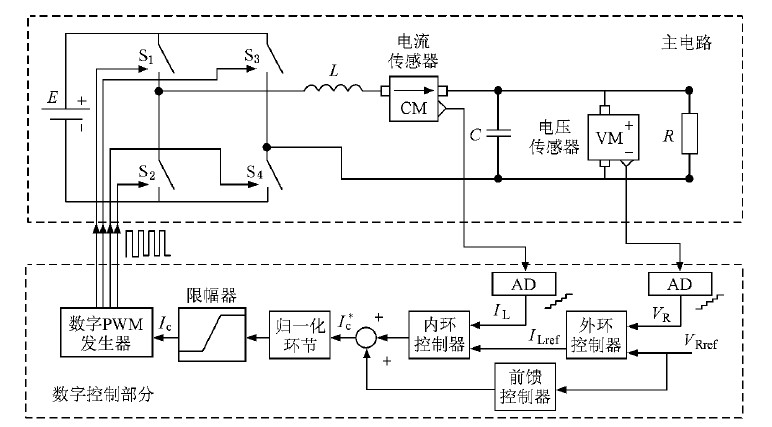
图1 数字控制单相全桥DC-AC 电压逆变电路系统图

维库PDF：单相全桥DC_AC电压逆变电路数字控制中的振荡现象分析.rar