浅谈OFDM系统定时同步技术的研究

　　同步技术（使两个或两个以上信号的某一参量(频率、相位、时间)保持固定关系的技术。 ）对各种数字传输技术来说十分关键，对于OFDM 系统更是如此。因为OFDM对同步误差十分敏感，同步性能的好坏直接影响到接收的性能，一旦同步性能不好，OFDM 的整体性能将会严重下降。

　　OFDM（Orthogonal Frequency Division Multiplexing）即正交频分复用技术，实际上OFDM是MCM Multi-CarrierModulation，多载波调制的一种。其主要思想是：将信道分成若干正交子信道，将高速数据信号转换成并行的低速子数据流，调制到在每个子信道上进行传输。正交信号可以通过在接收端采用相关技术来分开，这样可以减少子信道之间的相互干扰 ICI 。每个子信道上的信号带宽小于信道的相关带宽，因此每个子信道上的可以看成平坦性衰落，从而可以消除符号间干扰。而且由于每个子信道的带宽仅仅是原信道带宽的一小部分，信道均衡变得相对容易。

　　通常情况下，同步包括同步捕获和同步跟踪两个阶段。在同步捕获阶段，OFDM系统同步的主要任务是符号定时捕获和载波频偏（CFO）的捕获。关于符号定时和载波频偏估计算法，很多文献对此进行了探讨。提出了基于伪随机序列的定时捕获算法，但定时捕获通常是在频偏捕获之前完成的，因此当频偏较大时根本就看不到期望出现的峰值。作者基于一个由两个差分的OFDM训练符号组成的同步头，提出了一种联合的符号定时和载波频偏估计算法（简称为S&C算法）。该算法利用一个训练符号中两个相等的部分进行自相关来实现符号定时估计，因此频偏对它的影响很小，但是采用该算法进行估计时受循环前缀的影响将出现一种峰值平顶现象，这种现象使得估计出现较大的误差，因此严格地说采用这种算法只能起帧检测的作用，并不能完成真正的符号定时估计。参考文献[4]针对参考文献[3]的峰值平顶现象做了改进，在子载波数目较大时，定时测度出现一个单峰，但当子载波数目较少时会出现多峰值的现象，而且错误的峰值会大于正确时刻的峰值。

　　针对上面提到的问题，本文提出了一种新的符号定时捕获算法。这种算法采用了一个训练符号，通过对输出序列的自相关来解决大的频率偏差的问题，而且参考符号采用了正负变化。经过仿真证明该算法在多径信道中也能很好地工作。

　　1 OFDM系统描述

　　在OFDM系统的复基带等效模型中，发送端的OFDM复基带已调信号可表示为：

 

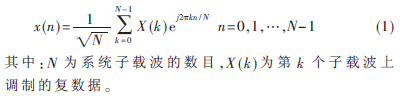
　　该信号经过信道传输后，接收端的符号定时偏移通常表示为接收信号的时延，载波的频率偏移通常表示为时域上的相位失真，因而具有符号定时偏移和载波频偏的OFDM系统的接收信号可表示为：

　　同步的主要任务是估计符号定时偏差τ和载波频偏ε，并通过补偿来消除或减弱同步误差对系统性能的影响。

　　2 算法描述

　　2.1 传统定时算法

　　对于OFDM的突发传输模式，接收端必须检测信号到来时刻，同时采用快速有效算法确定帧或符号的起始位置。通常用事先定义的训练符号结合相应的算法实现这一目的。SCHMIDL和COX基于[A,A]训练符号结构提出查找前后两个部分自相关峰值的定时算法[3]。可以通过频域在偶数子载波上调制一个复随机数，在奇数子载波上调制0，再通过做N点的IFFT（快速傅里叶逆变换）的方法生成时域上两个相同部分组成的训练序列[A,A]。生成训练数据的一个原则是训练数据的频谱特性和有效数据的频谱特性类似。同时必须考虑接收端判决系统复杂度。本文的分析和仿真中，频域训练数据全部来自QPSK调制数据，与有效数据的调制方式相同。采用SCHMIDL和COX定时算法，定时度量曲线会出现一个“模糊平台”，模糊平台的长度等于循环前缀的长度减去时延扩展长度。“模糊平台”，的产生增加了符号定时的不确定性。针对这种情况，参考文献[3]提出了用峰值点左右90％的两点求平均解决。MINN H在SCHMIDL和COX定时算法基础上提出了一种对定时度量做Ng+1长度的加窗平滑的方案。另外，基于[+A,+A,-A,-A]符号结构提出新的MINN H定时算法，这里A的长度是N/4，采用复随机数做N/4的IFFT生成。同样，定义N/4长度向量和新定时度量M（n）如下：

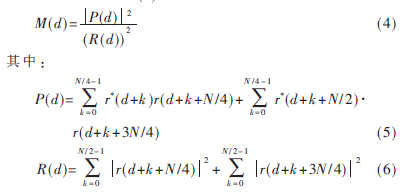
　　2.2 新定时方案的提出

　　在MINN H定时估计算法的基础上，对其定时测度进行了改进，定时估计算法的训练序列是参考HiperLAN/2的短训练序列的特点，其参考符号可以表示为[+A,+A,+A,-A]。从参考符号的结构可以看出，其参考符号也存在正负之差，这样在进行相关运算时也会出现尖峰，为了避免多峰值的出现，采用了相关累积的方法，对其多个相关值进行累加，这样在正确的定时时刻就会出现一个更高的峰值。该算法定时测度的表达式为：

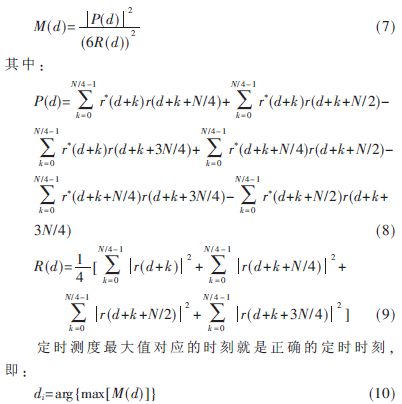
    其定时测度如图1所示。

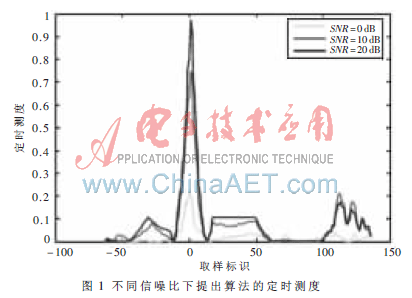
　　从图中可以看出，其定时测度为一尖峰，即使在信噪比很低的情况下，其正确定时时刻的峰值也高于其他分量，因此其具有较高的定时。

　　2.3 算法的性能

　　（1）频偏对定时估计的影响

　　一般来说，定时估计在频偏补偿之前完成，因此在进行定时估计时存在较大的频率偏差，因此频率偏差对定时估计算法的影响就显得尤为重要了。假设只受到噪声和频率偏差的干扰，则接收到的前导序列为：

 

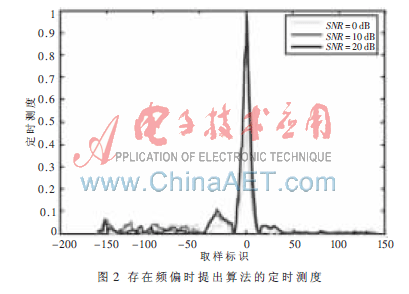
　　（2）噪声对定时估计的影响

　　假如只考虑噪声的影响，则由于噪声与训练序列具有较好的互相关性，所以η（d）项相对较小，再加上定时算法1是多个相关项的累加，因此受到的噪声干扰也相对较小，算法在信噪比较低的情况下也可以较好地完成定时估计。这一结果由图1也可以看出。

　　3 仿真结果

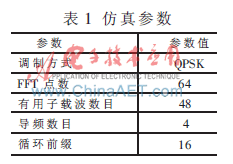
　　为了评估提出算法的性能，对算法进行了计算机仿真。仿真参数如表1所示。

　　所有算法估计的SNR值范围在0～20 dB，用估计误差的均值和估计误差的标准方差作为描述系统性能的指标，仿真环境为在加性白高斯噪声AWGN和多径环境。

　　多径采用Rayleigh衰落信道（循环前缀的长度大于信道时延值），6条多径。采用的多径功率时延分布如表2所示。

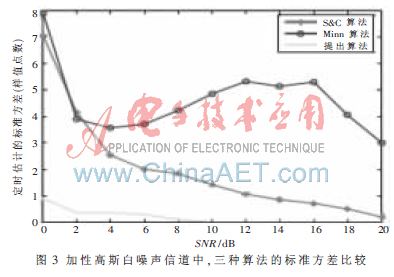
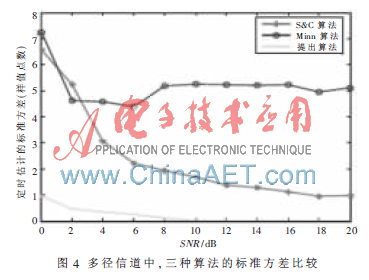
　　在加性高斯白信道中，对于不同的平均信道信噪比的情况下，对三种定时估计算法仿真得到的定时估计误差的标准方差如图3所示。从图3可以看出，本文提出的算法在信噪比大于10 dB时，其标准方差就已经接近于0了，也就是说可以准确地进行定时了，而定时S & C算法和H.Minn算法即使信噪比较高的情况下其标准方差仍然较大，只能完成帧同步，而本文提出的算法就可以完成帧同步和定时同步，而且定时的也比较高，在多径信道中三种算法的比较如图4所示，从图中可以看出，该算法的标准方差与高斯信道的基本一致，因此此算法在多径信道中仍然可以准确地完成定时同步。

　　本文提出了一种定时同步的估计算法，该算法利用了训练序列的特点，采用了自相关算法，可以不受频率偏差的影响，可以在频偏补偿之前进行定时估计，而且该算法不但在高斯信道中可以完成定时估计，而且在多径信道中也可以地完成定时估计，仿真结果也表明该算法对频率偏差具有较强鲁棒性，能够抗多径干扰。