分析滑动频率估计算法在微波测量液位中的设计与应用

　　随着科学技术的发展，频率估计在在液位测量器中的应用。是自动计量领域中重要的检测与控制参数之一，液位测量技术经过不断的发展，已经得到了很大的进步。目前提高频率估计的校正方法有很多，Rife插值法[3]利用两个采样点的比值来估计峰值的位置，但在噪声背景中，容易造成插值方向错误，引起较大的估计误差。参考文献[4]提出的FFT+FT谱连续细化法所需的计算量较大。基于上述分析可以发现，Rife比值法和三角形校正法在频谱校正上存在着各自的问题。本文在分析两者优缺点的基础上，结合两者的优势，提出了一种鲁棒性更强的滑动频率估计算法。该方法假设噪声是加性高斯白噪声，根据信噪比的变化情况，利用单次FFT后峰值谱线周围的多条谱线信息的三角形法和Rife比值法估计信号频率。

　　1 算法分析

　　1.1 Rife比值法

　　Rife比值法是利用主瓣峰顶附近两条谱线的幅度比值进行频谱校正的，信号的实际频率与估计频率之间的相对偏差δ为（加矩形窗）：

　　RIFE为开发和设计Web应用程序提供了另外一种途径。它基于Java平台构建，但它提供了所有需要的工具和AIPs用统一的风格，快速地实现所有 web程序各开发角色之间的任务联系。RIFE被设计成在整个开发周期中完全分离了开发角色之间的任务，每个developer,dba和 designer只需关注它们自己的任务，整个开发工作随时都可以很容易的与其它团队的工作相结合，使得这样子开发出来的将是一个松耦合的健壮的系统。 但是在有噪声的情况下，当|?啄|比较小时，可能会出现FFT频谱中其他谱线的幅度超过主瓣内次大值的情况，从而造成频率插值方向相反，引起较大的频率估计误差。当N一定时，不同信噪比下存在相应的临界值？啄0。当|δ|<δ0时，Rife比值法的频率估计误差比较大，特别是在|δ|接近于0时，频率估计误差将大大增加。

　　1.2 三角形法

　　三角形法（triangle method）是一种储量计算法。它的实质是把形状不规则的矿体，人为地简化为许多便于计算体积的三棱柱状体。即在储量平面图所圈定的矿体范围内，以直线连接各相邻勘探工程，把矿体分为一系列紧密连接的三角形块段。再依据三角形块段顶点的勘探工程资料，分别计算各地段的矿产储量。这种储量计算法不仅不能反映矿体的真实特点，而且计算过程繁杂，实际工作中很少应用。

　　三角形法主要是根据几何原理进行频谱校正，即用直线分别连接主瓣内峰值的左右谱线时， 可近似形成一个三角形，通过三角形的比例关系，可以得到谱线号修正量的式子am,即：

　　该方法校正原理简单，计算量小，较高。选取不同的n值，所获得的测量也不同。随着信噪比的增加，三角形法的测量有所增加，但提高幅度不大，受信噪比变化的影响较小。它不同于Rife插值法，整个频段误差的变化范围较小，稳定性好，但是频率估计误差比Rife插值法在|?啄|不接近0时大。

　　1.3 滑动频率估计算法

　　矩形窗Rife比值法和三角形法都只需要FFT的运算量，但在频率估计上都存在各自的问题。算法的具体过程如下：

　　（1）通过仿真实验，实时确定现场所在环境下的信噪比，记Rife比值法的偏差阈值为δ0，并查找P（k）的值P（m），其中P（k）=X2（k）。

　　（2）由于三角形法的频率估计误差稳定，因此估计的偏差am可信度高，当|am|<δ0，使用Rife插值法估计效果较差，此时使用三角形法进行频率估计，按照公式（4）可得到信号的实际频率估计。

　　（3）反之为|am|≥δ0时，三角形法对实际频率的估计误差大于矩形窗Rife插值法，因此，使用Rife插值法进行频率估计，按照公式（2）可得到信号的实际频率估计。

　　可见，Rife比值法与三角形法的有效结合构成了滑动频率估计算法，根据次大值与值的幅度比值来预先设定偏差阈值δ0。根据|δ|的不同，即频率所在位置的不同，采用不同的估计方法。

　　2 仿真实验

　　为了验证所提算法的有效性，作如下仿真实验。

　　这里采用锯齿波LFMCW雷达测量液位，根据被测频率与目标距离之间的关系，采用3种方法对实际距离进行测量。设定液面与天线的距离为0~20 m，信噪比为12 dB。对所选的几个被测距离分别采用Rife比值法、三角形法（n=3）、滑动频率估计算法进行估值（δ0=0.12），各被测点进行了1 000次测量得到平均值R和均方根误差σR如表1所示。

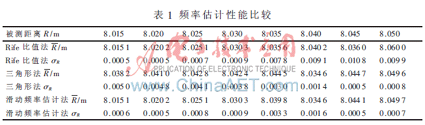
　　从表1可以看出，当被测距离接近离散频谱谱线所对应的距离时（R=8.045），即|?啄|较小时，Rife插值法的距离测量均方根误差大大增加，为0.010 8。而此时的三角形法距离测量的均方根误差较小，为0.000 5，且整个变化区间内，均方根误差变化较小。但是当被测距离远离离散频谱谱线所对应的距离时，三角形法的估计误差比Rife插值法大（R=8.020）。而本文所提出的滑动频率估计算法结合两者的优势，根据|δ|的不同选取不同的估计方法，在整个所观测的测量范围内，距离估计的均方根误差较小，测量较高。

　　下面来观察一下距离估计误差与数据输入长度N（N=16，32，64，128，256，512，1 024）之间的关系。图1为N不同时三种估计方法的性能比较。设R=4.176 m,SNR=15 dB，其他条件同上。由仿真结果可以看出，当N取值较小时， Rife算法的频率估计较低，而三角形法的频率估计较高，且在所观察的变化区间内，三角形法的频率估计性能稳定，而Rife算法在N较大的时候，频率估计效果较好。在结合两者优点的基础上，本文提出的滑动频率估计算法在所观察的区间内受数据长度的变化影响较小，测距较高，而且运算简单，计算量不大。

　　再来观察一下不同估计方法随信噪比的变化情况。此时R=14.565 m，其他条件同上。图2是三种估计方法的距离估计的均方根误差与信噪比的变化情况。从图中可以看出，Rife插值法在整个信噪比区间均方根误差变化较大，受信噪比的影响较大，当信噪比较低时，Rife插值法引起了更大的估计误差。而本文所采用的滑动频率估计算法，克服了上述两种算法的不足，在所观测的整个信噪比变化区间内，距离测量的均方根误差都较小，测量高。

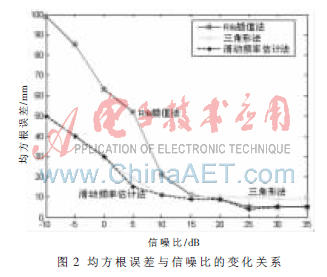
　　本文通过对Rife比值法和三角形法的研究，建立了一种随信噪比变化的频谱校正模型。该方法有效地融合了多条谱线信息的贡献，根据频率所在位置的不同选取不同的估计方法，避免了Rife算法的插值方向错误问题。实验结果显示，该方法的测量高，即使在噪声背景中，微波液位测量的误差也能满足工程需要，并且频谱校正受数据长度的变化影响较小。