滑模控制感应加热电源在电流仿真分析中应用

 

　　1 引 言

　　高频逆变电源的可靠工作是感应加热的一个重要发展方向，分别从主电路，控制电路，驱动电路的设计出发，seo对提高高频逆变电源的工作状态下的可靠性进行了深入的研究，通过理论设计计算，计算机仿真和试验等方法，得出了高频逆变电源的研究结果。在对一般的感应加热电源电路结构分析的基础上，选择了适合功率和频率进一步提高的主电路拓扑。采用不可控整流，逆变调功的方式，使逆变器工作于略高于谐振频率的方式。保护吸收电路采用了简化的电流控制阻抗和阻容吸收的方式，来保护IGBT感应加热的安全。在对无源器件的高频模型分析基础上，指出了高频应用下无源器件的选择原则，分析了逆变器布局的要求，给出了逆变器布局的结果。

　　采用滑模控制方式的逆变器与传统控制方式相比，具有良好的动态特性、鲁棒性以及在电源和负载大范围变化时能保证系统稳定性的优点。滑模控制方式要求全状态变量反馈，且需要相应的基准参考量，增加电路设计的复杂性，所以一般的滑模控制方式大多停留在理论分析和仿真阶段。

　　滑模控制与常规控制的根本区别在于控制的不连续性，即一种使系统"结构"随时间变化的开关特性。由于功率变换器中开关元件的存在，使滑模变结构控制理论得到广泛应用。

　　2 负载回路的数学模型

　　图1为串联谐振感应加热系统电路结构图，其中负载回路由电容Cc、感抗L和电阻R串联形成振荡回路。假设直流电压Vdc连续，C远大于振荡电容Cc,变压器变比N为1.

　　假定初始电流为零，负载电路上电压为VS,则输出电流i0和电容电压vc的时域方程为：

　　由于采用软开关技术，系统的开关频率等于振荡频率。串联谐振电路的输入电压vs可由以下开关状态决定：

　　为方便地表述逆变器运行状态，引入一个新的离散变量M(k)如下；

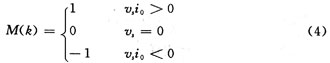
　　图2为运行状态描述，(a)为开关导通状态；(b)为输出电流io，整流电流∣io∣，参考电流Iref，每半周期电流峰值Io；(c)为运行状态(1：输入功率模式，0：自由衰减模式)；(d)变压器二次侧电压Vs。

　　于是，式(3)可改写成为：

　　该式表明，运行状态一旦确定，Vs的幅值为Udc，符号由i0(t)决定，式(5)中T=π／ωd是半个振荡周期，每半个振荡周期的输出电流峰值Io和电容电压Vc可用离散变量表示。由于Q远大于1，可认为；Vc比Io滞后π／2，可得差分方程：

　　电容电压Vc离散状态的动态峰值由式(7)自身表示。将式(7)代入式(6)，就可得负载回路的离散电流状态方程：

　　M=1电路工作在输入功率模式下，谐振环节电流持续增加；
　　M=0电路工作在自由衰减模式下，谐振环节电流不断减小；
　　M=-1电路工作在再生功率模式下，谐振环节电流较自由衰减模式减小更快；
　　本文只使用前2种工作模式，即在功率输入与自由衰减2种状态运行，变量u(k+1)表示电流控制强度，实际取值为{1，0.5，0}。根据以上分析得到的离散电流动态模型，可分析电流控制器设计方案。
　　3 滑模变结构电流控制策略

　　本节讨论一种应用比例积分滑模的电流控制技术。目的是使在稳态下输出电流峰值的Io有一个较小的电流偏移量时，能够较为准确地跟随于期望的参考电流Iref，在阶跃输入时可以有快速的瞬态响应和较小的超调量。
　　引入滑模变结构控制理论(the theory of VariableStructure Control，VSC)。滑模控制（sliding mode control, SMC）也叫变结构控制，本质上是一类特殊的非线性控制，且非线性表现为控制的不连续性。这种控制策略与其他控制的不同之处在于系统的"结构"并不固定，而是可以在动态过程中，根据系统当前的状态（如偏差及其各阶导数等）有目的地不断变化，迫使系统按照预定"滑动模态"的状态轨迹运动。由于滑动模态可以进行设计且与对象参数及扰动无关，这就使得滑模控制具有快速响应、对应参数变化及扰动不灵敏、无需系统在线辨识、物理实现简单等优点。滑模变结构控制的原理，是根据系统所期望的动态特性来设计系统的切换超平面，通过滑动模态控制器使系统状态从超平面之外向切换超平面收束。系统一旦到达切换超平面，控制作用将保证系统沿切换超平面到达系统原点，这一沿切换超平面向原点滑动的过程称为滑模控制。

电流控制的离散滑动模型可由式(8)表述。
　　滑模切换函数的选取影响系统的动态品质，本文采用电流误差积分滑模面，切换函数可表述如下：

　　S为离散滑模切换函数，Ki为积分增益，Ie=Iref-Io为电流误差。
　　电流控制器的控制律为：

　　感应加热系统电路参数L，C和R已定，则滑模控制系统响应完全由Ki决定。采样保持器检测输出电流峰值，并保存1个振荡周期，与参考信号比较并产生误差信号。电流控制器的输出决定下一个运行状态，当过零检测器检测到过零信号时就切换开关状态。从滑模控制系统稳定性、快速响应性、较好的鲁棒性和负载变化不敏感性等方面考虑，可以用较大的增益Ki来快速补偿偏移量。增益Ki设计的恰当，就能有效消除基频偏移量，得到稳定的输出电流。
　　3.1 积分器增益Ki的确定

　　对于离散准滑模系统，准确到达切换面常是不可能的，这里假设：

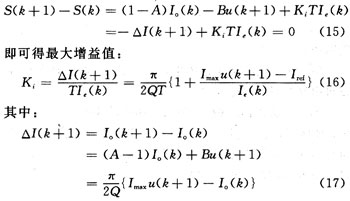
　　考虑到当Iref=Imax或Iref=0时为电流控制的极限值，且u(k+1)的值为{1，0.5，0)，可确定增益值范围：

　　3.2 切换面吸引性分析

　　系统进入准滑动模态的到达条件：

　　要保证实现滑模控制，必须使比例积分滑模控制切换面具有可到达性。考虑u(k)的控制作用，由图2可以看出，当输出电流连续2个T小于参考电流值Iref时，u(k+1)的值为1，系统处于功率输出状态，使负载电流峰值上升；当大于Iref两个T时，u(k+1)的值为0，系统就切换为自由振荡状态；由于负载消耗，电流峰值必然会小于Iref，通过u(k+1)的计算，系统又切换至功率输出状态。由上述分析可知，状态空间中任意工作点都可在控制律的作用下到达式(14)确定的切换面，即切换面具有可到达性。
　　3.3 稳定性分析

　　定义Lyapunov函数：

　　4 仿真结果分析

　　本文采用Matlab语言，编写M函数对上述模型进行仿真。参数选取如下：
　　R=0.2 Ω，L=12.0μH，Cc=0.2μF
　　计算可知电路谐振频率为100 kHz；增益Ki的值取为10000。设参考电流为60 A，初始电流值为0，N=4，则如图3所示。

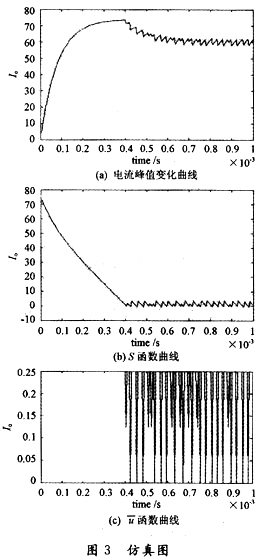
　　5 结语

　　针对串联谐振感应加热电源逆变器，建立逆变器的负载回路离散数学模型，分析比例积分滑模控制电流控制器切换面参数的选择条件、可达性和滑模存在性及稳定性；选择适当的增益后，可使滑模控制对输出负载变化具有良好的快速性和鲁棒性。根据此模型，使基于DSP控制策略容易实现。