一种基于EZW改进算法的图像压缩方法探讨

　　近年来，随着更大面阵的图像传感器（包括红外和可见光）的应用，图像生成设备的输出数据率越来越高，而数据存取及传输信道带宽相对较窄，这两者的矛盾越来越尖锐。如何实时对高输出数据率的图像进行压缩始终是当前图像压缩领域研究的难点也是重点。目前已研究出的一些压缩方法，都存在不同程度的局限性，如DPCM压缩率不高；矢量量化（VQ）的计算复杂度随着维数的上升而急剧增加；而JPEG是迄今广为使用的国际压缩标准，但在量化误差较大时会产生方块效应。20世纪80年代在傅里叶变换基础上发展起来的小波变换，有效实现了信号、图像的空频转换，图像经过小波分解后可以去除相关特性，实现能量的重新分配，使近似信息集中在低频区域，细节信息反映在高频区域。根据小波系数的这一特点，很容易实现图像数据的压缩。JPEG-2000图像压缩标准、MPEG-4视频压缩标准已经将小波变换列入其中。

　　图像的小波变换就是以原始图像为初始值，不断将上图像分解为4个子带的过程，每次得到的4个子带图像，分别代表频率平面上不同的区域，它们分别含有上图像中的低频和垂直、水平及对角线方向的边缘信息。其中，子带HLn表示了水平方向的高频、垂直方向的低频成分，子带LHn表示了水平方向的低频、垂直方向的高频成分，而子带HHn则表示了水平和垂直方向的高频成分。从多分辨率分析出发，一般每次只对上的低频子图像进行再分解。图像小波变换示意如图1所示。

　　2 EZW算法

　　在图像的小波系数矩阵中，用"零树"来描述这种依频率特性递减的数据分布特性。在"零树"中，通过区分零树根（ZTR）、孤零（IZ）、正重要系数（POS）和负重要系数（NEG）这几种不同性质小波系数的方法，来实现变换编码的过程。

　　嵌入式小波零树编码EZW（Embedded Zero tree Wavelet）算法，就是利用零树的一种高效的小波图像压缩算法。实际中采用零树与逐次逼近量化技术SAQ（Successive Approximation Quantization）相结合，构成EZW编码算法。其主要步骤如下：

　　对图像小波变换的研究表明，一些较小的高频系数几乎应该不再包含图像信息，可以对这些信息进行噪声抑制，而不会对图像的重构质量有大的影响。所以当逐次逼近的阈值落入这一相关区域时，可以停止对小波系数的扫描。量化编码前将这一部分系数作为噪声进行滤波处理，这也是对原算法可以进行改进的地方。

　　基于以上分析，提出EZW的改进算法如下：

　　（1）图像小波系数的重新排列。为便于将图像小波系数转化到信号处理领域，并通过对信号的噪声分离来求得原图像中的噪声冗余，需要对代表原图像的小波系数矩阵进行矢量排列，使其转化为一个新的信号向量C.具体方法是：首先对子频带LLn的小波系数矩阵按列排列成一个一个新的列向量c1,然后按照HLn,LHn,HHn,…，HL1,LH1,HH1的顺序依次生成列向量c2,c3,c4,…，c3n-1,c3n,c3n+1,令C=[c1;c2;c3;c4;c3n-1;c3n;c3n+1],则生成信号向量C.

　　（2）信号分解。将信号C进行小波分解，进而将其分离为近似信息与噪声细节。令C=S+U,其中S为近似信息，U为噪声细节，则WTC=WTU+WTS.WTC为小波变换算子；WTU对应小波基中低通滤波部分，其还原的为近似信息；WTS对应小波基中低通滤波部分，其还原的为噪声细节。此处的噪声细节不能直接从信号C中直接去除，而是应该利用其参数作为下一步阈值处理的依据。

　　（6）主扫描。

　　（7）副扫描。

　　对于（6）、（7）中的扫描问题，保持原算法（2）、（3）中的扫描及逐次逼近量化方式。另外，考虑图像小波系数的零树结构特性，对每扫描中出现的零树根节点，与其对应位置的更高频带的小波系数就不再参与扫描编码，这样可以显着地提高扫描编码的效率。所以，每次扫描的过程实质上就是对重要系数的不断量化细化的过程。

　　（9）送熵编码。

　　4 仿真实验结果及分析

　　为验证算法的有效性，本文中采用的是256×256的lena图像，以Matlab 7.1为实验仿真平台。首先由函数命令imread读入图像信息，读入后得一个大小为256×256的像素矩阵；用wavedec2函数对所读取的二维图像信息进行小波分解（这里取分解层数为N=3），选取小波基为"db1"小波。图2为图像小波分解后各层信息。对于本文设定的具体小波分解参数，可以得到由频到各个方向高频的共10个小波系数矩阵，按照第3节中第（1）步所述的原则将其转化为一新的信号向量C.用离散信号的分解函数dwt对其进行信噪分离。图3显示的即为分解出的噪声信息。

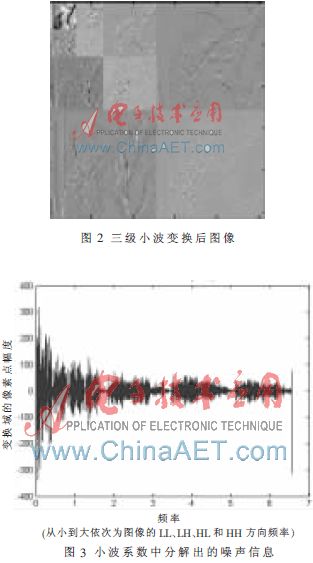
　　由噪声样本计算标准差，得σ=14.28,按照式（4）可求得阈值δ=17.98.对小波系数进行硬阈值化，可以得到优化以后的小波系数Cg,其中置零系数百分比perf0=86.36%.为进一步确定Cg是否对原始图像产生了失真，可以通过小波逆变换重构出图像的灰度信息。图4为原始图像和阈值化处理后的重构图像。

　　由图4可以看出，两幅图像在视觉效果上已经没有区别，说明了阈值化处理的可行性。

　　然后，针对图像小波域系数存在"零树"结构的特点，通过编写逐次逼近量化的Matlab程序，分别应用原有算法和改进算法对lena图像进行压缩处理。图5为经过相同的扫描次数，两种算法图像压缩后所重构的复原图像。

　　表1给出了对应情况下的图像质量评价标准：峰值信噪比（PSNR）和压缩比（CR）。在仿真中，扫描终止时低频阈值为TL=32,高频阈值为TH=16.

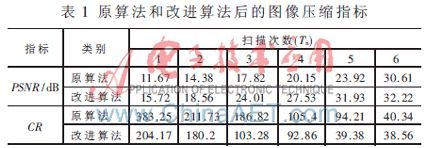
　　通过分析实验结果可以得出，改进算法无论是在相同扫描次数下复原图像的信噪比，还是在相近信噪比下图像的压缩比（体现为相邻斜对角参数的比较），较之原算法都获得了较大改善，这说明算法改进是成功的。不足之处在于编码过程中增加了小波系数的再处理，对低频和高频分阈值量化，这对编、解码设备都提出了更高要求。但从缩短码流和节约信道资源方面，这些都是可以接受的。

　　本文在分析和研究EZW图像压缩算法的基础上，提出了小波系数噪声分离、阈值化小波系数、分阈值量化低频和高频信息的EZW改进算法。实验结果表明，改进算法性能和压缩比都有了提高，不失为一种行之有效的图像压缩算法，同时它也为小波变换应用于图像压缩编码提供了一种新的思路。