电容耦合二阶LTCC带通滤波器的分析与设计

     摘要： 提出了一种谐振腔间通过电容耦合和基于LTCC技术的集总带通滤波器（带通滤波器是指能通过某一频率范围内的频率分量、但将其他范围的频率分量衰减到极低水平的滤波器，与带阻滤波器的概念相对）结构。该方法在输入输出端引入反馈电容来改善阻带性能， 同时利用等效集总电路并采用图解和数学方法来解释传输零点的变化， 给出了设计此类滤波器的一般步骤。

　　0 引言

　　近年来， 无论是军用电子整机、通信设备还是民用消费类的电子产品都迅速向小型化、复杂化、轻量化、多功能化和高可靠性的方向发展。

　　而以LTCC (低温共烧陶瓷， Low Temperature CofiredCeramic) 为基础的结构设计可有效减小器件体积， 是实现元器件向小型化、片式化、高可靠性和低成本方向发展的有效途径。滤波器是决定通信系统性能的重要元器件。为此， 许多论文都提出通过在阻带内加入传输零点来提高滤波器的阻带衰减性能， 从而获得陡峭过渡带。

　　本文给出的设计方法涉及三个方面： 是通过设计一种滤波器结构来提高阻带性能。该滤波器采用谐振单元耦合， 并在输入输出端引入并联反馈电容来在阻带内引入传输零点。传输零点的个数与位置可以通过耦合电容和电感控制。

　　第二是通过滤波器结构等效集总电路来写出导纳矩阵， 再用图解和数学方法解释传输零点情况。这对快速设计这类滤波器具有指引作用。

　　第三是通过仿真滤波器来证明理论的正确性。

　　1 LTCC滤波器的物理布局

　　本设计给出的滤波器的空间拓扑结构如图1所示， 其中图1 (a)、(b) 分别为不同角度观察的滤波器三维图， 其中介质为Rogers RT/duroid5880， 介电常数为εr=2.2， 损耗角正切为0.0009，介质为4层， 每层为500μm， 水平面积为3mm×18mm， 导体材料采用银。金属层从下至上分别为1至5层， 其中下层和上层为接地金属层(为使结构图更清楚， 图1中隐藏了上层金属层)， 中间三层为电路拓扑， 其端口馈电在第三层上， 为电容馈电方式， 可与第二层和第四层电容板形成接入电容C3和C4， 调节馈电板的边长C_w1， 可以改变电容C3与C4。加长接入和接出电容板， 可使两块电容板靠近， 并引入耦合电容C6， 电容板的间距为len， 未加长时， 两电容板的间距为2400μm。通过在左右两个谐振腔的电容板之间加入耦合电容板， 可以引入电容C5， 调节电容板边长C_w2可控制耦合电容C5的大小。

　　电感在第三层， 由一根金属线构成， 可通过半径为50μm的通孔接地， 金属线的宽度为200μm，调节金属线的长度L_len可改变电感L1与L2的大小。曲线形金属线在滤波器第二层， 为电感L3。

　　电容为第四层和第二层电容板与上下地形成的接地电容， 第四层与第二层电容板通过通孔相连，一个正方形电容板的面积为3mm×3mm。为使结构更加简单和便于调试， 该结构的所有电容板都采用正方形结构。

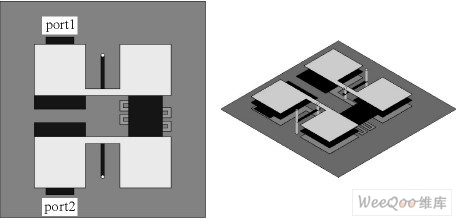
图1 LTCC滤波器三维图。

　　2 集总电路设计原理

　　本设计的滤波器等效电路如图2所示， 通过图2可以看出， 该电路可分为上下两个子网络，其滤波器的导纳矩阵为：

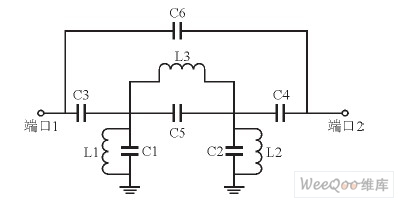
图2 有反馈电容的带通滤波器等效电路。

　　其中， y11′， y12′， y21′， y22′是滤波器没有反馈电容C6的导纳矩阵元素。通过导纳矩阵Y可知，形成传输零点的位置可由下列方程确定：

　　采用节点导纳分析法， 可以得到没有加入反馈电容C6时的导纳矩阵元素：

　　其中：

　　由于使用的是对称结构， 所以， c1′=c2′=cl1′=l2′=l这样， 将上式代入(3)， 可得到四阶方程：

　　(4) 式中， 因为c>c5， l<m所以方程系数均为正， 即方程有两个正的传输零点频率。

　　一般情况下， 在中心频率处， 都希望传输所有能量， 此时的谐振器阻抗应该为零。其中心频率为：

　　而如果方程根满足：

　　则传输零点分别位于通带的两边。从(4) 式可以看出， 通过C5可以改变传输零点的位置。

　　当c5=0时， 方程(3) 可以改写为：

　　其中， c1′=c1+c3 c2′=c2+c4由方程(7) 可知， 左右两曲线的交点即为通带两边传输零点的位置。

　　为了解释该理论， 本文设计的带通滤波器中心频率为f0=2.45 GHz。设计可用插入损耗法， 并采用通带波纹0.2 dB的二阶切比雪夫低通原型。

　　通过阻抗变换公式可以得到图1中各元件值： L1=L2=1.1nH， C1=C2 =3.78 pF， C3=C4 =1.34 pF， l3=5.87 nH， 反馈电容C的取值可通过图3所示的传输零点位置来确定， 本设计中取C=0.06 pF。通过电路仿真软件可以得到图4所示的S参数仿真图。

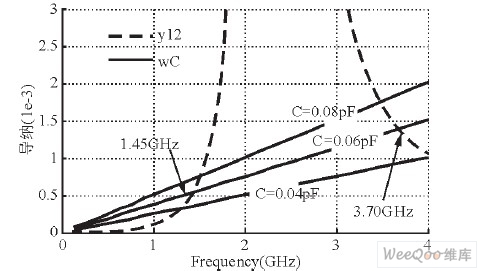
图3 传输零点的位置图。

图4 传输特性S曲线仿真图。

　　由图3所示可以看出， 反馈电容C6=0.06 pF时， 两个导纳曲线相交于1.45 GHz和3.70 GHz处，表明滤波器在这两个频率处形成了传输零点， 图4中圈线为未引入反馈电容C6时的二阶切比雪夫带通滤波器的传输特性S曲线， 实细曲线为引入反馈电容(C=0.06 pF) 后在通带两边形成的一对传输零点的传输特性S曲线， 可见， S曲线传输零点的位置与导纳方程的解符合的很好。

　　3 滤波器的实现与仿真结果

　　在没有引入耦合电容C6时， 其接入接出电容板间距为2400 μm， 设计时可将两电容板加长并靠近。图5为两电容板间距从2000 μm减小至1600μm时的S参数仿真图， 从图5中可以看到， 两电容板越近， 耦合电容C6越大， 两传输零点距中心频率越近， 而对通带则影响不大， 通带情况几乎没有变化， 这与第二部分的理论一致。

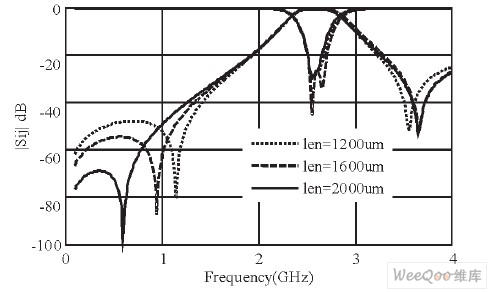
图5 变化接入电容板间距的滤波器S参数仿真图。

　　通过改变矩形金属线电感长度L_len所得到的S参数仿真图如图6所示。从图6中可以看到，增大L_len， 中心频率与两传输零点均向低频偏移， 插入损耗减小， 滤波器相对带宽变宽， 通带内两谐振频率点相距越远， 波纹也越大。

　　由于滤波器（凡是有能力进行信号处理的装置都可以称为滤波器）结构中的所有电容板边长相同，都为3000 μm (用C_w表示)， 故可得到图7所示的改变C_w的S参数仿真图。由图可见减小电容板边长对滤波器的影响与增大直线形金属线电感长度对滤波器的影响完全一致。

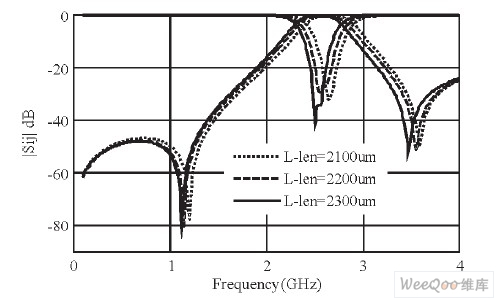
图6 变化电感长度的滤波器S参数仿真图。

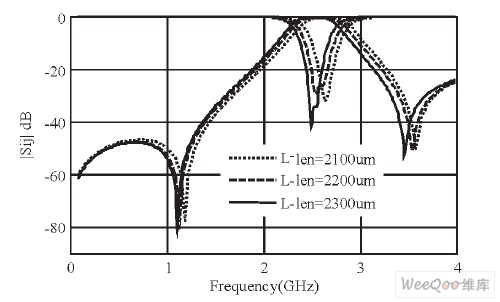
图7 变化所有电容板边长的滤波器S参数仿真图。

　　4 结束语

　　本文给出了一种小型化的新型电容耦合式LTCC带通滤波器的设计方法。仿真结果显示，在中心频率处， 通带内的插入损耗小于1.0 dB，回波损耗大于20 dB。通过多阶频率方程可以有效地得出传输零点的位置， 而且仿真结果与理论分析一致。