0 引 言
加减速控制是数控系统的技术。常用的加减速控制方法有直线加减速、指数加减速、S形曲线加减速等方法。直线加减速方法和指数加减速方法虽然计算量小,编程简单,但是在加减速阶段存在加速度突变的现象,导致机床产生剧烈振动,不适合用于数控机床的高速加工。常用S形曲线加减速通过限制加加速度来控制加速度的突变现象,然而传统的S形曲线加减速控制方法利用多项式表示法将整个速度规划分为5个或7个阶段,然后在每个阶段内进行讨论,计算量大,编程复杂。
本文通过在直线加减规划之后,通过滑动平均滤波器来解决加速度的跳变问题,在不改变原有程序结构的情况下,实现了和S形曲线等效的加减速效果。
1 基于滑动平均滤波的速度规划算法
基于滑动滤波技术的速度规划算法就是在传统的直线加减速的算法后面串联一个滑动平均滤波器对速度进行平滑的速度规划方法。这种速度规划方法分为两大部分:直线加减速规划部分和滑动平均部分(图1)。

图1 基于滑动平均滤波的速度规划结构图
1.1 直线加减速
考虑在ent[S/(υmaxTs)]>na(Ts为采样时间,na为加速(减速)所需的采样周期个数,S为加工路径长度,υmax为速度值)的情况下,直线加减速的轮廓曲线如图2所示。
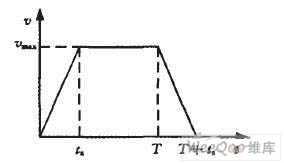
图2 直线加减速规划速度轮廓图
假设第i个采样周期末的瞬时速度为υ(i),第i个采样周期的位置增量为△S(i),运动的总长度为S,加速度为a,则有

同时可以知道,加速度a在t分别为0、ta、T、T+ta的时刻存在跳变,这种跳变导致机床的振动。
1.2 滑动平均滤波
在直线加减速规划后面串联一个长度L(L是滑动平均滤波器的阶次(长度))的滑动平均滤波器,通过对前L个速度数据进行累加平均,然后随着新的规划数据的加入,老的速度规划值被移出。记滑动滤波器的第i个采样周期末的速度为υ(i),加速度为a(i)那么可以得到


2 几个相关定理
定理1(位置不变性) 对直线加减速做滑动平均滤波规划和直线加减速规划的位置相等。
证明:记直线加减速规划、直线加减速滤波后的位置分别为

因为υ(i)=0,i>n,所以
从以上推导还可以看到,滤波器只需要速度信息,而不需要速度是如何规划的,所以滑动滤波器不仅适用于直线加减速规划,对其他方法也适用,于是可以得到下面的推论。
推论1 对任何速度规划法得到的速度进行滑动平均滤波,其规划位置均保持不变。
定理2( 等效性) 对直线加减速做滑动平均规划和S形加减速规划等效。
证明:
(1)S形加减速的加速度。S形加减速规划分为5段:加加速段、减加速段、匀速段、加减速段、减减速段。假设加速度从0增达到值和从值减小至0的时间相等,加速时间ts=2nsTs,减速时间td=2ndTs,其中,ns表示加速时,加速度从。达到值的采样周期数,nd表示减速时,加速度从0达到值时的采样周期数,速度为υmax,加速段的加加速度和加速度值分别为Js、αsmax,减速段的加加速度和加速度值分别为Jd、αdmax。
假设第i个采样周期末时刻的速度为υ(i),加速度为α(i),位置增量为ΔS(i),运动的总长度为S。则有

从式(12)可以看出,加速度α(i)是分段函数,但在相邻区间是连续的,即不存在跳变,有效地克服了机床的振动。
(2)基于滑动平均滤波速度规划的加速度。不失一般性,只考虑i∈[0 L]的情形,其余时刻类推。
由式(7)可知,当0≤i≤L时有
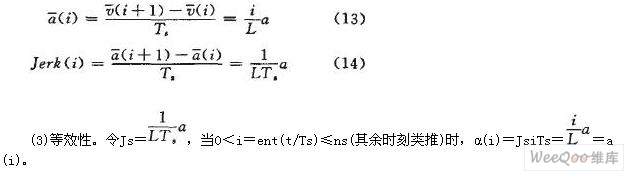
(3)等效性。令Js=,当0<i=ent(t/Ts)≤ns(其余时刻类推)时,α(i)=JsiTs==a(i)。
(4)规划结束及滤波补偿。在直线加减速规划后要做滤波补偿,将滤波器里的速度值完全放出,以保证位置不变。
(5)运动结束。当滤波器里的值完全放出后,表示全部运动结束,并将所有标志置为结束。
可以看出,对直线加减速滑动滤波和S形加减速的加速度是等效的,从而可知本方法的加速度也是连续变化的,可以有效克服机床的振动。
3 基于滑动平均滤波的速度规划算法的软件设计与实现
该方法的软件实现分为以下几个步骤(图3):

图3 本文方法程序流程图
(1)初始化。在运动开始前,初始化运动开始/结束标志,规划开始/结束标志,滤波开始/结束标志,滤波延迟补偿标志,滤波器数组等。
(2)运动开始。将运动标志及相关标志置为开始。
(3)正常规划及滤波。① 做直线加减速规划;②对直线加减速规划得出的速度做滑动平均处理。
(4)规划结束及滤波补偿。在直线加减速规划后要做滤波补偿,将滤波器里的速度值完全放出,以保证位置不变。
(5)运动结束。当滤波器里的值完全放出后,表示全部运动结束,并将所有标志置为结束。
4 实验结果及分析
为了验证该本文算法的有效性,在本所自主开发的数控系统GJ-310上做了相关实验,其实验条件和结果分别如下:
(1)直线加减速实验。直线加减速所采用的参数如下:速度υmax=10m/min,Ts=2ms,加减速时间为80ms。图4中曲线3是从(0,0)运行到(30,0)mm的速度轮廓曲线。
(2)S形加减速实验。直线加减速所采用的参数如下:速度υmax=10m/min,Ts=2ms,加减速时间为120ms。图4中曲线2是从(0,0)运行到(30,0)mm的速度轮廓曲线。
(3)直线加滑动滤波加减速实验。直线加减速参数和实验(1)完全相同,滤波器长度L=20,图4中曲线3是该方法从(0,0)运行到(30,0)mm的速度轮廓曲线。
比较图4中的三条曲线发现,S曲线速度规划和本文提出的速度规划方法均有效地解决了加减速在启/停时加速度存在跳变的问题。同时发现只要选择适当滤波器长度,可以得到和S形加减速规划等效的速度曲线。

图4 三种方法的实验结果
5 结 论
本文揭示了直线加减速会使机床产生振动的本质是加速度产生跳变,用滤波技术解决了直线加速度的跳变问题,探索了一种速度规划新方法。本文先从原理上证明了基于滤波原理的速度规划和传统的S形加减速是等效的,然后给出了如何实现这一方法的软件实现步骤和实验结果。本文方法还具有如下优点:①易于实现;②向前兼容性好,无需改变以前软件结构;③可以和其他速度规划方法结合使用,因为本文方法只需要原始速度信息,不对原始速度的产生有附加限制。研究结果为采用滤波技术来解决原有数控系统的振动间题提供了理论基础和软件实现方法。
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。