电力系统数字滤波器优化设计与算法实现

　　摘要：本文分别用凯塞窗函数法和切比雪夫逼近法，在MATLAB环境下实现了面向电力系统应用的FIR数字低通滤波器的设计和仿真，得出基于切比雪夫逼近法设计的数字低通滤波器为理想，之后讨论了滤波器阶次和权向量对纹波的影响。介绍了基于DSP器件设计数字滤波器的算法实现和部分程序代码。

　　1、概述

　　在数字滤波器家族中，FIR 滤波器与IIR 滤波器相比，由于具有严格的线性相位和因果稳定性等一系列优点，因而得到了广泛应用。可以用窗函数法、频率取样法和切比雪夫逼近法等方法设计FIR 数字滤波器。

　　在设计数字滤波器时，可以用软件仿真和硬件实现的方法。MATLAB 软件使用简单、方便、易编程、语言简练，可以方便地进行数字滤波器的设计、仿真和性能分析。在MATLAB环境下，采用切比雪夫逼近原理设计的面向电力系统应用的FIR 数字低通滤波器，具有严格的线性相位，可以获得接近理想的幅频特性。随着半导体技术的飞速发展，用 DSP 器件可以实现高速数字滤波器。讨论基于DSP的数字滤波器算法实现具有现实意义。

　　2、用MATLAB 设计面向电力系统应用的FIR 数字低通滤波器

　　2.1 滤波器设计指标

　　2.2 滤波器设计方法

　　基于“切比雪夫一致逼近”理论，利用MATLAB信号处理工具箱（Signal ProcessingToolbox）提供的remez函数，实现Parks McClellan算法，使实际滤波器的幅频响应地拟合理想滤波器的幅频响应，使它们之间的误差化，以此获得较好的通带和阻带性能，并能准确地指定通带和阻带的边缘，且在频域范围内具有等波纹特性，故利用remez函数设计的FIR数字滤波器有时被称为滤波器。首先确定滤波器的估计阶次N0、归一化截止频率向量f0、通带和阻带的理想滤波器幅度向量A0以及权向量weigh。相应的程序代码如下：

　　调用remez 函数等设计指定指标的FIR 数字低通滤波器，并输出滤波器的幅频特性曲线，其程序代码如下：

　　依据设计指标，用凯塞窗（kaiser）函数设计电力系统应用的低通FIR 滤波器，相应的程序代码为：

　　从滤波器的幅频特性曲线可以看出：设计同样指标的面向电力系统应用的低通 FIR 滤波器，用kaiser 窗函数法则需要更高的阶次（33 阶），而用切比雪夫逼近法则只需要28阶；此外，相对于kaiser 窗函数法设计的滤波器，基于切比雪夫逼近理论设计的滤波器的幅频衰减曲线阻带具有等纹波特性。

　　2.3 切比雪夫FIR 滤波器的阶次N 和权向量weigh 分别对纹波产生的影响赋于 N0 不同的值N0＝20：1：30调用语句：[b,delta]=remez(N,f0,A0,weigh)函数返回纹波值delta 向量，即delta=[0.0114 0.0078 0.0065 0.0066 0.0050 0.0034 0.0037 0.0031 0.0020 0.0021 0.0019]由图3 可知，要改善纹波就以增加滤波器阶次为代价。N＝28 对应的是满足纹波要求的阶次。用同样的方法改变滤波器的权向量，得出由remezord函数产生的weigh=[1 1]组合也是的，其它组合下都有滤波器的纹波值delta﹥0.0020。比如，weigh=[1 2]组合产生的纹波值delta=0.0033﹥0.0020。

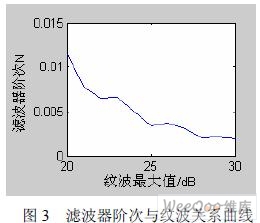
　　3、数字低通FIR 滤波器的DSP 算法实现

　　为了说明问题，以N＝3 的简单情况描述程序流程。3 阶FIR 数字滤波器的差分表达式为：

　　y(n)=h(0)x(n)+ h(1)x(n-1)+ h(2)x(n-2) （1）

　　程序的步是设置 RAM 的两组存储区，一组存放采样数据，另一组存放滤波器系数，如表1 所示。初始状态下，采样数据存储区设置为0。滤波器存储区存放滤波器设计与分析工具所求得的数据。初始化后按如下步骤执行：

　　处理个采样数据。读取第 1 个采样数据，把数据RAM 区中N 个单元的数据都移动1 个单元，将空出的1 个单元存放新读入的数据，然后计算输出：

　　y(1)=h(0)x(1)+ h(1)x(0)+ h(2)x(-1)，将计算结果输出。

　　处理第 2 个数据。重复数据移位操作，计算输出：

　　y(2)=h(0)x(2)+ h(1)x(1)+ h(2)x(0) ，将计算结果输出。

　　处理第 3 个数据。重复数据移位操作，计算输出：

　　y(3)=h(0)x(3)+ h(1)x(2)+ h(2)x(1) ，将计算结果输出。

　　处理第 4 个数据。重复数据移位操作，计算输出：

　　y(4)=h(0)x(4)+ h(1)x(3)+ h(2)x(2) ，将计算结果输出。

　　......

　　处理第n 个数据。重复数据移位操作，计算输出：

　　y(n)=h(0)x(n)+ h(1)x(n-1)+ h(2)x(n-2)，将计算结果输出。

　　经过上述计算，滤波器系数存储区内容不变，采样数据存储区内容变化如表2 所示。

　　由上述过程可以得出 FIR 滤波器运算程序流程，如图4 所示。

　　以TMS320C54XX 系列DSP 器件为基础实现FIR 数字滤波器的程序段如下所示。其中，AR4 存储采样数据，AR5 存储滤波器系数。

　　4、总结

　　通过与基于凯塞（kaiser）窗的FIR 低通滤波器幅频特性相比，以及对滤波器阶次和权向量对滤波器纹波的影响的分析，得出基于切比雪夫逼近原理设计的面向电力系统应用的FIR 低通滤波器既有好的衰减特性又有好的边缘频率，滤波器的阶次也可以预先设计，因而比较接近理想特性。

　　以 3 阶FIR 滤波器设计为例，讨论了基于DSP 算法设计与部分程序代码。相信随着DSP 器件的不断发展，基于DSP 设计面向电力系统的FIR 数字滤波器的技术必将取得长足的进步。