基于提升小波变换的模糊图像融合算法研究

　　引言

　　图像融合指综合和提取两个或多个图像的信息，从而获得对同一场景或目标更为准确、全面和可靠的图像，使其更加适合人眼感知或计算机后续处理。常用的图像融合的分类方法是基于图像表征层的划分，将图像融合分为像素级、特征级和决策级3级。图像的小波分解是一种像素级图像融合普遍采用的方法，利用小波非冗余性使图像经小波分解后数据量不会增大；同时小波分解具有方向性的特性，可针对人眼对不同方向的高频分量具有不同分辨率这一视觉特性，在图像融合时获得效果更佳的融合图像。基于提升方法的小波变换又称第2代小波变换，它既保持传统的小波时频局部化等特性，又克服其局限性。提升的实现形式给出小波完全的空间域解释，它具有许多优良特性：结构简单、运算量低、原位运算、节省存储空间、逆变换可直接反转实现，可逆的整数到整数变换，便于实现。采用提升格式的coif5小波变换进行图像融合处理。针对低频和高频系数不同的特点运用不同的融合规则。仿真结果表明模糊图像融合效果良好。

　　2 原理与算法

　　2．1 提升小波变换原理

　　提升算法给出双正交小波简单而有效的构造方法，使用基本的多项式插补获取信号的高频分量，通过构造尺度函数获取信号的低频分量。由提升方法构成的小波变换分为分裂、预测和更新3个步骤：

　　(1)分裂(Split)将原始信号分为两个互不相交的子集和，通常是将一个数列分为偶数序列和奇数序列，即

　　(2)预测(Predict)根据数据间的相关性，可用sj-1预测dj-1。故可采用一个与数据集结构无关的预测算子P，使得dj-1=P(sj-1)，这样就可以用子数据集sj-1代替原始的数据集sj。若用子集dj-1与预测值P(sj-1)的差值去代替dj-1，则此差值反映两者的逼近程度。如果预测合理，则差值数据集所包含的信息比原始子集dj-1包含的信息要少得多。预测过程的表达式如下：

　　(3)更新(Update)经步骤(1)产生子集的某些整体特征(如均值)可能与原始数据并不一致，为了保持原始数据的整体特征，需要一个更新过程。经小波提升，可将信号sj分解为低频部分sj-1和高频部分dj-1；对于低频数据子集sj-1可再进行相同的分裂、预测和更新，将sj-1进一步分解为dj-2和sj-2，…如此下去，经过n次分解后，原始数据sj用小波表示为{sj-n，dj-n，dj-n+1，…，dj-1}其中，sj-n％代表信号的低频部分；dj-n，dj-n+1，dj-1，则是信号从低到高的高频部分。

　　(4)重构重构数据时的提升公式与分解公式相同，改变计算次序和符号即可。

　　式中，Merge即“合并”，是将分裂后的子集sj-1和dj-1，重构为初始信号sj。

　　图1为利用第2代小波变换分解和重构的示意图。利用不同的预测算子P和更新算子U可以建立不同的小波变换。

　　2．2 小波基的选择

　　对同一图像，采用不同的小波基对其进行分解会产生不同的结果，由于不同的小波基具有不同的性能指标。小波基函数的正则性越高，其分辨率越高，等效滤波器组的幅频响应旁瓣越低；其消失距阶数R越高，对应滤波器的低频拖尾衰减越快；对于正交小波，如果尺度函数和小波是紧支撑，则滤波器呈现FIR特性，其分解和重构算法可以通过FIR滤波器组实现；当尺度函数和小波对称时，滤波器呈现广义线性相位，缺乏该性质将会引起相位失真。因此，小波基的选取要兼顾小波的正交性、对称性、光滑度和正则性等。

　　选取Daubechies构造的coiflets小波函数，它具有coifN (N=1，2，3，4，5)一系列，coifles小波具有双正交性、紧支撑性、近似对称性等优点。coifN比dbN对称性更好，其支撑长度与db3N相同，其消失矩阶数与db2N相同。为分析不同的小波基对变换结果的影响，分别采用传统的haar、coif5以及提升格式db2小波、coif5小波对两幅模糊图像进行融合并仿真。

　　3 融合规则

　　每个源图像在进行二维提升小波分解后分别得到由各层的细节子图像和一个分解层的近似子图像构成的子图像系列。由于图像的细节子图像和近似子图像包含的信息不同，针对其不同特点，分别采用不同融合规则进行融合。

　　3．1 低频系数融合规则

　　由于低频分量对恢复图像质量影响很大，可融合为：

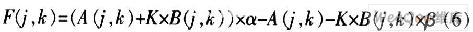
　　式中，k，α，β为加权因子。

　　(A(j，k)+K×B(j，k))×α为取两幅图像的加权均值，影响融合后图像的能量，对融合后图像的亮度起决定作用；(A(j，k)-K×B(j，k)×β为取两幅图像的加权差值，包含两幅图像的模糊信息。因子K调节两幅图像的占优比例，使两幅亮度不同的图像达到均衡。随着α增大，图像加亮；随着β增大，图像的边缘加强。

　　对于不同图像，适当调整K、α及β，可消减模糊边缘，同时确保不会丧失过多边缘信息。

　　3．2 高频系数的融合规则

　　高频系数融合采用局部方差准则。局部方差定义为：

　　Std(X，Y)=1／MN∑∑[X(i,j)-Y]2 (7)

　　式中，X为M×N的区域；X(i，j)为区域X中像素点(i,j)的灰度值；Y为区域X的灰度平均值。

　　局部方差可反映区域信息含量，融合图像是对同一目标不同时刻(或采用不同成像设备所成的像)的反映，因此，可选取信息含量更丰富的图像组成融合结果，得到该目标的更多信息。

　　3．3 融合步骤

　　采用小波分析的图像融合算法的一般步骤如图2所示。

　　对二维图像进行Ⅳ层的小波分解，终将得到(3N+1)个不同频带，其中包含3N个高频带和一个低频带。融合的基本步骤：(I)对源图像分别进行提升小波分解；(2)对各分解层分别进行融合处理，采用不同的融合算子对各分解层的不同频率分量进行融合处理。对于低频分量，采用加权平均法进行融合。对于高频分量，采用局部方差准则处理其系数；(3)对得到的系数矩阵进行反变换即得到输卅图像。

　　4 仿真结果

　　分别采用传统的haar、coif5以及提升格式db2小波、coifs小波对两幅模糊图像进行融合。图3为仿真结果，可看到基于提升coif5的图像效果明显好于传统的haar和coif5小波。从计算量和实时性考虑，所采用算法的计算量比传统的小波大大减少，实时性也较传统小波有很大提高。

　　5 结束语

　　探讨一种基于提升小波变换的图像融合算法，提升小波的构造不依赖于傅里叶变换，应用它进行图像融合可提高处理速度，节约内存空间，提高实时性。试验表明，使用提升小波使融合图像自然、边缘清晰，同时保留了多输入原图像的有用信息。适合任意尺寸的图像融合。今后的工作将进一步研究融合规则和融合方法，使图像融合算法能够在模糊图像恢复、自动目标识别与跟踪、遥感、医学图像处理、智能机器人、复杂智能制造系统等领域有更广泛的应用。