传递函数的幅度近似

　　1．频率归一化
　　在设计滤波器的传递函数和研究滤波器的幅频特性近似问题时，为了简化计算，使计算规格化和通用化，通常采用频率归一化的处理方法。所谓频率归一化，是将传递函数复频率s＝α十jω除以基准角频率ω_λ，得到归一化复频率

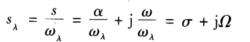
　　对于低通、高通滤波器，一般采用截止角频率（1），作为基准角频率；对于带通、带阻滤波器，一般采用中心角频率00作为基准角频率。在用波特图描述滤波器的幅频特性时，通常横坐标用归一化频率Ω代替ω。
　　2．传递函数的幅度近似
　　在设计、研究滤波器时，通常是按通频带分类，分为低通滤波器、高通滤波器、带通滤波器、带阻滤波器。在这4种滤波器中，常将低通滤波器作为设计滤波器的基础，高通、带通、带阻滤波器传递函数可由低通滤波器传递函数转换过来，因此，低通原型传递函数的设计是其他传递函数设计的基础。
　　如图 l 所示为理想低通滤波器的幅频特性。但是这种理想的幅频特性不可能采用有限个元件组成的网络来实现，只能采用一个有理函数来近似实现。因此，需要对滤波器的幅频特性提出一个允许的变化范围，如通带增益波动范围、阻带必须达到的衰减、过渡带带宽和衰减特性等，如图2所示为幅度近似的低通幅频特性。寻找一个合适的有理函数来满足对滤波器幅频特性提出的要求，寻找这个合适的有理函数即是滤波器的幅度近似。