常用的差错控制方法

　　常用的差错控制方法有奇偶校验法、循环冗余校验法和汉明码等。这些方法用于识别数据是否发生传输错误，并且可以启动校正措施，或者舍弃传输发生错误的数据，要求重新传输有错误的数据块。

　　1． 奇偶校验法

　　奇偶校验法是一种很简单并且广泛使用的校验方法。这种方法是在每一字节中加上一个奇偶校验位，并被传输，即每个字节发送九位数据。数据传输以前通常会确定是奇校验还是偶校验，以保证发送端和接收端采用相同的校验方法进行数据校验。如果校验位不符，则认为传输出错。

　　奇校验是在每个字节后增加一个附加位，使得“1”的总数为奇数。奇校验时，校验位按如下规则设定：如果每字节的数据位中“1”的个数为奇数，则校验位为“0”若为偶数，则校验位为“1”。奇校验通常用于同步传输。而偶校验是在每个字节后增加一个附加位，使得“1”的总数为偶数。偶校验时，校验位按如下规则设定：如果每字节的数据位中“1”的个数为奇数，则校验位为“1”；若为偶数，则校验位为“0”。偶校验常用于异步传输或低速传输。

　　校验的原理是：如果采用奇校验，发送端发送的一个字符编码（含校验位）中，“1”的个数一定为奇数个，在接收端对接收字符二进制位中的“1”的个数进行统计，若统计出“1”的个数为偶数个，则意味着传输过程中有1位（或奇数位）发生差错。事实上，在传输中偶然—位出错的机会多，故奇偶校验法经常采用。

　　然而，奇偶校验法并不是一种安全的检错方法，其识别错误的能力较低。如果发生错误的位数为奇数，那么错误可以被识别，而当发生错误的位数为偶数时，错误就无法被识别了，这是因为错误互相抵消了。数位的错误，以及大多数涉及偶数个位的错误都有可能检测不出来。它的缺点在于：当某一数据分段中的一个或者多位被破坏时，并且在下一个数据分段中具有相反值的对应位也被破坏，那么这些列的和将不变，因此接收方不可能检测到错误。常用的奇偶校验法为垂直奇偶校验、水平奇偶校验和水平垂直奇偶校验。

　　2． 垂直奇偶校验

　　垂直奇偶校验是在垂直方向上以列的形式附加上校验位。假设数据格式及其发送顺序如图1所示，则垂直奇偶校验的编码规则如图2所示。

　　图1 垂直奇偶校验时

　　图2 垂直奇偶校验法举例

　　数据格式及其发送顺序

　　式中，m为码字的定长位数，n为码字的个数。

　　设垂直奇偶校验的编码效率为R，则：

　　垂直奇偶校验又称为纵向奇偶校验，它能检测出每列中发生的奇数个错误，偶数个错误，因而对差错的漏检率接近1／2。

　　3． 水平奇偶校验

　　水平奇偶校验是在水平方向上以行的形式附加上校验位。假设数据格式及其发送顺序如图3所示，则水平奇偶校验的编码规则如图4所示。

　　图3 水平奇偶校验时数据格式及其发送顺序

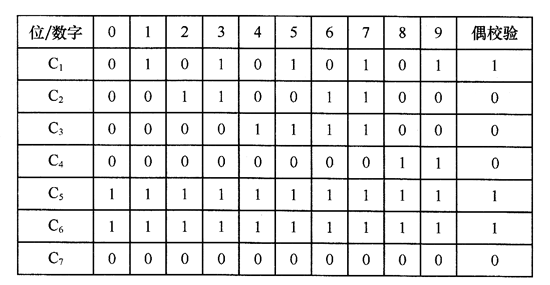
　　图4 水平奇偶校验法举例

　　式中，m为码字的定长位数，n为码字的个数。

　　设水平奇偶校验的编码效率为R，则：

　　水平奇偶校验又称为横向奇偶校验，它不但能检测出各段同一位上发生的奇数个错误，而且还能检测出突发长度≤m的所有突发错误，其漏检率要比垂直奇偶校验法低，但是实现水平奇偶校验时，一定要使用数据缓冲器。

　　4． 水平垂直奇偶校验

　　水平垂直奇偶校验是在结合水平奇偶校验和垂直奇偶校验的基础上形成的一种校验方法。它是在一批字符传送之后，另外增加一个称为“方块校验字符”的检验字符，方块校验字符的编码方式是使所传输字符代码的每个纵向列中位代码的“1”的个数成为奇数（或偶数）。

　　假设数据格式及其发送顺序如图5所示，如果水平和垂直方向上都使用偶校验，则水平垂直奇偶校验的编码规则如图6所示。

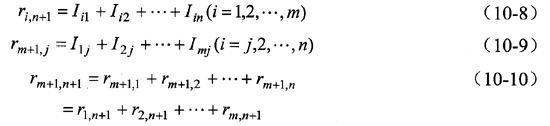
　　图5 水平垂直奇偶校验时数据格式及其发送顺序

　　图6 水平垂直奇偶校验法举例

　　式中，m为码字的定长位数，n为码字的个数。

　　设水平垂直奇偶校验的编码效率为R，则：

　　水平垂直奇偶校验又称为纵横奇偶校验。它能检测出传输过程中发生的所有3位或3位以下的错误、奇数个错误、大部分偶数个错误以及突发长度≤m＋1的突发错误，可使误码率降至原误码率的百分之一到万分之一，有较强的检错能力，但是有部分偶数个错误不能检测出来。水平垂直奇偶校验还可以自动纠正差错，使误码率降低2～4个数量级，适用于中、低速传输系统和反馈重传系统，被广泛用于通信和某些计算机外部设备中。

　　5． 循环冗余校验法

　　循环冗余校验（CRC，Cyclic Redundancy Check）法由分组线性码的分支而来，主要应用于二元码组。它是利用除法及余数的原理来作错误侦测（Error Detecting）的。

　　这是一种比较、安全的检错方法，能够以很大的可靠性识别传输错误，并且编码简单，误判概率很低，但是这种方法不能够校正错误。循环冗余校验法在通信系统中得到了广泛的应用，特别适用于传输数据经过有线或无线接口时识别错误的场合。下面重点介绍循环冗余校验法

6． CRC法的工作原理

　　循环冗余校验法是一种较为复杂的校验方法，它不产生奇偶校验码，而是将整个数据块当成一个连续的二进制数据M（x），在发送时将多项式M（x）用另一个多项式（被称为生成多项式G（x））来除，然后利用余数进行校验。从代数的角度可将M（x）看成是一个多项式，即M（x）可被看作系数是0或1的多项式，一个长度为昭的数据块可以看成是x^m-1到x⁰的m次多项式的系数序列。例如一个8位二迸制数10110101可以表示为：1x⁷＋0x⁶＋1x⁵＋1x⁴十0x³＋1x²＋0x＋1。

　　实际应用时，发送装置计算出CRC校验码，并将CRC校验码附加在二进制数据M（x）后面一起发送给接收装置，接收装置根据接收到的数据重新计算CRC校验码，并将计算出的CRC校验码与收到的CRC校验码进行比较，若两个CRC校验码不同，则说明数据通信出现错误，要求发送装置重新发送数据。该过程也可以表述为：发送装置利用生成多项式G（x）来除以二进制数据M（x），将相除结果的余数作为CRC校验码附在数据块之后发送出去，接收时先对传送过来的二进制数据用同一个生成多项式G（x）去除，若能除尽即余数为0，说明传输正确；若除不尽说明传输有差错，可要求发送方重新发送。其工作过程如图7所示。

　　图7 循环冗余校验法的工作方法

　　采用循环冗余校验法，能检查出所有的单位错误和双位错误，以及所有具有奇数位的差错和所有长度小于等于校验位长度的突发错误，能查出99％以上比校验位长度稍长的突发性错误。其误码率比水平垂直奇偶校验法还可降低1～3个数量级，因而得到了广泛采用。

　　7． 相关计算

　　CRC校验码的计算是一种循环过程。CRC校验的计算包括了要计算其CRC值的数据字节以及所有前面的数据字节的CRC值。数据块中的每一被校验过的字节都用来计算整个数据块的CRC值。

　　从数学角度来看，CRC校验码就是利用所谓的生成多项式G（x）去除一个多项式M（x）（数据字节）来获取的。CRC校验码就是相除后所得的余项。

　　要计算阴位数据块M（x）的CRC校验码，生成多项式G（x）必须比该多项式短，且生成多项式G（x）的高位和低位必须为1。CRC的基本思想是：将CRC校验码加在数据块的尾部，使这个带CRC校验码的多项式能够被生成多项式除尽。当接收设各收到带校验码的数据块时，用生成多项式去除，如果有余数，则数据传输出错。

　　计算CRC校验码和带CRC校验码的发送数据T｛x｝的算法如下：

　　（1）设G（x）为r阶，在数据块M（x）的末尾附加r个零，使数据块变为m＋r位，则相应的多项式为xrM（x）；

　　（2）按模2除法用对应于G（x）的位串去除对应于x^rM（x）的位串。

　　（3）按模2减法从对应于x^rM（x）的位串中减去余数（总是小于等于1）。结果就是要传送的带循环冗余校验码的数据块，即多项式T（X）。

　　8. 计算举例

　　下面举例说明CRC校验码和带CRC校验码的发送数据T（X）的计算过程，如图8所示。

　　图8 CRC校验码以及发送数据T（X）的计算

　　设数据块M（x）的二进制表示形式为1101011011，生成多项式G（x）=x⁴＋x＋1，则G（x）的二进制表示形式为：10011，数据块：1101011011，除数：10011，附加4个零以后形成的数据块：11010110110000，传输的数据块为：1 10101 101 1 1 1 10。

　　显然，如果利用G（x）对发送数据T（X）执行新的CRC计算，所得结果为零。CRC校验的这种独特性质可以用来检测串行数据传输中的错误。CRC校验的—大优点是识别错误的可靠性，即使有多重错误，也只需要少量的操作就可以识别。16位的CRC就适用于校验4000字节长的数据块的完整性。超过此长度时，性能明显下降。射频识别系统中传输的数据块都比4000字节短，这意味着除了16位的CRC以外，也可以使用12位和8位的CRC。

　　9． 常用的CRC生成多项式

　　CRC在数据通信中得到了广泛的应用。表2列出了已经成为国际标准的四种CRC生成多项式，其中CRC－12用于字符长度为6位的情况，其余三种则用于字符长度为8位的情况。CRC－32出错的概率比CRC－16低10^-5倍。由于CRC－32的可靠性，把CRC－32用于重要数据的传输十分合适，所以CRC－32在通信、计算机等领域应用十分广泛。在一些UART通信控制芯片内都采用了CRC校验码进行差错控制；以太网卡芯片、MPEG解码芯片中，也采用CRC－32进行差错控制。

　　表2    常用的CRC生成多项式

　　欢迎转载，信息来源维库电子市场网（www.dzsc.com）