FIR滤波器理论

　　带有常系数的FIR滤波器是一种LTI数字滤波器。z阶或者长度为z的∏R输出对应于输入时间序列x［n］的关系由一种有限卷积数量形式给出，具体形式如下：

　　其中从f［0］≠0—直到f［L－1］≠0均是滤波器的z阶的系数，同时也对应于ΠR的脉冲响应。对于LTI系统可以更为方便地将（3，2）表示成z域内的形式：

　　其中F（z）是FIR的传递函数，其z域内的形式如下：

　　图1给出了z阶LTI型FIR滤波器的图解。可以看出，ΠR滤波器是由一个“抽头延迟线”加法器和乘法器的集合构成的。传给每个乘法器的操作数就是一个FIR系数，显然也可以称作“抽头权重”。过去也有人将FIR滤波器称为“横向滤波器”，就是说它的“抽头延迟线”结构。

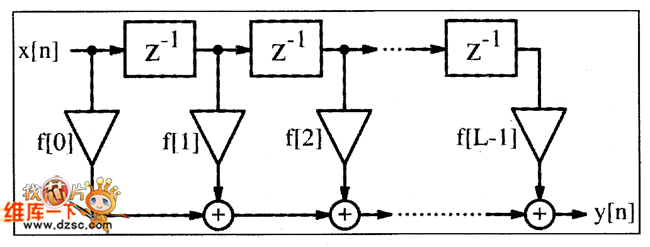
　　图1 直接形式的FIR滤波器

　　（3．4）中多项式F（z）的根确定了滤波器的零点。仅有零点存在也就是FIR经常被称作“全零点滤波器”的原因。在第5章我们将讨论∏R滤波器中重要的一类（叫作CIC滤波器），它是递归的，但也是FIR。这是可能的，因为递归部分产生的极点已经被滤波器的非递归部分消除了。有效极点／零点图就变得只有极点了，也就是全零点滤波器或者是FIR。注意：非递归滤波器均是FIR，但是递归滤波器却可以是FIR或者是IIR。图2说明了这一关系。

　　图2 结构和脉冲长度之间的关系
　　欢迎转载，信息来源维库电子市场网（www.dzsc.com）