LC滤波器考虑寄生电容时的设计

　　作为近似，电感和电容都看作集总参数的纯电抗元件，大多数实际电容接近于理想电抗；而另一方面，电感都不是理想的，在很多情况下，这可能造成危害。除了严重的电阻损耗外，还会出现寄生电容，包括线圈绕组之间的匝间电容以及与骨架相关的杂散电容等。电感线圈的等效电路如图1所示。

　　图1 电感的等效电路图

　　由于分布电容的存在，实际电感特性将变成一个并联谐振回路特性。若该线圈与外接电容并联，则外接电容值可相应减小，以抵消分布电容的影响。

　　在串联谐振回路中电感两端跨接的分布电容，会引起并联谐振，导致出现频率响应零点。如果电感的自然谐振频率很低，零点甚至会出现在通带内，严重破坏所期望的频率响应。

　　为了确定实际电感线圈的有效电感，让线圈与外接电容谐振于期望频率，采用标准谐振公式计算其有效电感量。有效电感也可以使用下式计算：

　　式中，LT是真实（低频）电感量；f是期望的工作频率；五是电感线圈的自谐振频率。当F接近f，时，Leff急剧增加，在fr处，Leff变为无穷大。式（8．11）的函数表示的曲线见图2。

　　为了补偿串联谐振电路中分布电容的影响，实际电感量L，适当减小一点，使得由式（8．11）得到的Lm为需要的值。实际串联谐振回路的Q值为：

　　式中，QL是电感线圈的品质因数，它取决于串联损耗（即ωLT／RL）。因此，有效品质因数Q由于分布电容的影响会有所下降。

　　分布电容的大小取决于骨架和绕组的机械参数，且分布电容也随机械应力等而改变。因此，为了获得的稳定性，分布电容要尽可能小。

　　另一种形式的寄生电容是电路节点与地之间的杂散电容。这些杂散电容对高频应用和高阻节点是特别有害的。对于低通滤波器，因为电路节点已有并联到地的电容，所以这些杂散电容一般可以忽略，特别是在阻抗比较小的时候。

　　图2 随频率变化的等效电感

　　图3所示是一个椭圆函数带通滤波器的一部分。当电路中的某些节点没有出现接地电容时，这些节点是高阻抗节点，其杂散电容会引起问题。

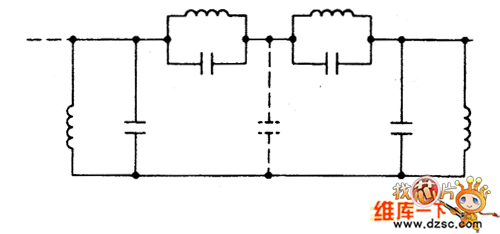
　　图3 一个椭圆函数带通滤波器