台达伺服电机在金属切削机床的应用

时间：2007-09-26

　　机床的驱动电机包括进给伺服电机和主轴伺服电机两类。机械制造商在选购电机时担心切削力不够，往往选择较大规格的马达，这不但会增加机床的制造成本，而且使之体积增大，其结构布局不够紧凑。因此，一定要通过具体的分析计算，选择规格的电机。

　　一、进给驱动伺服电机的选择

　　1. 原则上应该根据负载条件来选择伺服电机。在电机轴上所有的负载有两种，即阻尼转矩和惯量负载。这两种负载都要正确地计算，其值应满足下列条件:

　　1)当机床作空载运行时，在整个速度范围内，加在伺服电机轴上的负载转矩应在电机连续额定转矩范围内，即应在转矩速度特性曲线的连续工作区。

　　2)负载转矩，加载周期以及过载时间都在提供的特性曲线的准许范围以内。

　　3)电机在加速/减速过程中的转矩应在加减速区(或间断工作区)之内。

　　4)对要求频繁起，制动以及周期性变化的负载，必须检查它的在一个周期中的转矩均方根值。并应小于电机的连续额定转矩。

　　5)加在电机轴上的负载惯量大小对电机的灵敏度和整个伺服系统的将产生影响。通常，当负载小于电机转子惯量时，上述影响不大。但当负载惯量达到甚至超过转子惯量的5倍时，会使灵敏度和响应时间受到很大的影响。甚至会使伺服放大器不能在正常调节范围内工作。所以对这类惯量应避免使用。推荐对伺服电机惯量Jm和负载惯量Jl之间的关系如下:

1≤Jl/Jm＜5

　　2. 负载转矩的计算方法加到伺服电机轴上的负载转矩计算公式，因机械而异。但不论何种机械，都应计算出折算到电机轴上的负载转矩。通常，折算到伺服电机轴上的负载转矩可由下列公式计算:

Tl=(F*L/2πμ)+T0

    式中,Tl:折算到电机轴上的负载转矩(N.M)
        F:轴向移动工作台时所需要的力
       L:电机轴每转的机械位移量(M)
         To:滚珠丝杠螺母，轴承部分摩擦转矩折算到伺服电机轴上的值(N.M)
         μ:驱动系统的效率

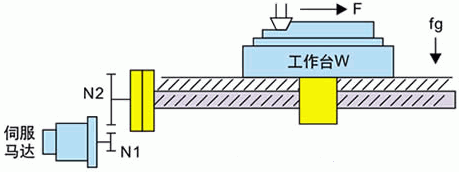
图1 工作台进给示意图

　　F取决于工作台的重量，摩擦系数，水平或垂直方向的切削力，是否使用了平衡块(用在垂直轴)。如果是水平方向，F轴的值由上图例给出。

无切削时: F=μ*(W+fg),切削时: F=Fc+μ*(W+fg+Fcf)

    式中,W:滑块的重量(工作台与工件)Kg
       μ:摩擦系数
         Fc:切削力的反作用力
         fg:用镶条固紧力
         Fcf:由于切削力靠在滑块表面作用在工作台上的力(kg)即工作台压向导轨的正向压力。

计算转矩时下列几点应特别注意。

　　(a) 由于镶条产生的摩擦转矩必须充分地考虑。通常，仅仅从滑块的重量和摩擦系数来计算的转矩很小的。请特别注意由于镶条加紧以及滑块表面的误差所产生的力矩。

　　 (b) 由于轴承，螺母的预加载，以及丝杠的预紧力滚珠接触面的摩擦等所产生的转矩均不能忽略。尤其是小型轻重量的设备。这样的转矩回应影响整个转矩。所以要特别注意。

　　(d) 摩擦转矩受进给速率的影响很大，必须研究测量因速度工作台支撑物(滑块，滚珠，压力)，滑块表面材料及润滑条件的改变而引起的摩擦的变化。已得出正确的数值。

　　(e) 通常，即使在同一台的机械上，随调整条件，周围温度，或润滑条件等因素而变化。当计算负载转矩时，请尽量借助测量同种机械上而积累的参数，来得到正确的数据。

　　3. 负载惯量的计算。由电机驱动的所有运动部件，无论旋转运动的部件，还是直线运动的部件，都成为电机的负载惯量。电机轴上的负载总惯量可以通过计算各个被驱动的部件的惯量，并按一定的规律将其相加得到。

　　1) 圆柱体惯量如滚珠丝杠，齿轮等围绕其中心轴旋转时的惯量可按下面公式计算:

J=(πγ/32)*D4L(kg cm2)

如机构为钢材，则可按下面公式计算:

J=(0.78*10-6)*D4L(kg cm2)

    式中,γ:材料的密度(kg/cm2)
       D:圆柱体的直经(cm)
        L:圆柱体的长度(cm)

　　2) 轴向移动物体的惯量工件，工作台等轴向移动物体的惯量，可由下面公式得出:

J=W*(L/2π)2 (kg cm2)

式中,W:直线移动物体的重量(kg)
L:电机每转在直线方向移动的距离(cm)

　　3) 圆柱体围绕中心运动时的惯量如图所示:

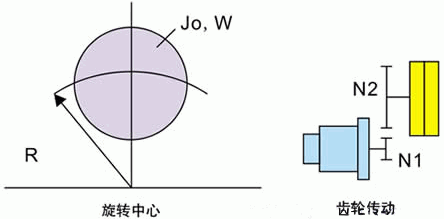
图2 圆柱体围绕中心运动时的惯量

属于这种情况的例子:如大直经的齿轮，为了减少惯量，往往在圆盘上挖出分布均匀的孔这时的惯量可以这样计算:

J=Jo+W*R2(kg cm2)

    式中,Jo:为圆柱体围绕其中心线旋转时的惯量(kgcm2)
         W:圆柱体的重量(kg)
         R:旋转半径(cm)

　　4) 相对电机轴机械变速的惯量计算将上图所示的负载惯量Jo折算到电机轴上的计算方法如下:

J=[(N1*N1)/(N2*N2)>*Jo

式中,N1、N2:为齿轮的齿数

　　4. 电机加速或减速时的转矩

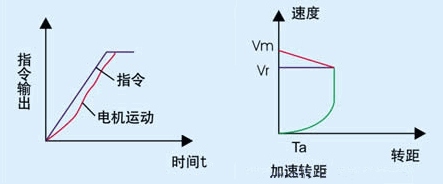
图3 电机加速或减速时的转矩

　　1) 按线性加减速时加速转矩计算如下:

Ta=(2πVm/60*104) *1/ta(Jm+JL)(1-e-ks。ta)
Vr=Vm{1-1/ta.ks(1-e-ksta)

    式中,Ta:加速转矩(N.M)
         Vm:快速移动时的电机转速(r/min)
         Ta:加速时间(sec)
         Jm:电机惯量(N.m.s2)
         JL:负载惯量(N.m.s2)
         Vr:加速转矩开始减少的点
         Ks:伺服系统位置环增益(sec-1)

　　电机按指数曲线加速时的加速转矩曲线如下图:

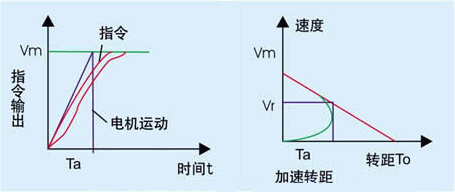
图4 电机按指数曲线加速时的加速转矩曲线