1、μ律压扩
μ律压扩的数学解析式：
其中：x为输入信号的归一化值；y为压扩后的信号。对话音信号编码，常采用μ=255，这样适量化信噪比改善约24dB。
2、A律压扩
其特性可表示为：
很明显，小信号时为线性特性，大信号时近似为对数特性。这种压扩特性常把压缩、量化和编码合为一体。A律可用13段折线逼近（相当于A=87.6），便于用数字电路实现。
13段折线的压缩特性如下图。过程为：
步：把x（x>0 部分）划分为不均匀的8段。分点取在V/2处，然后每段都是剩下部分的1/2。；依次取第八段为V~V/2,第七段为V/2~V/4；段为V/128~0。
第二步：把每段均匀划分为16等份，每一份表示一个量化级，显然8段共16x8=128= 
个量化级，需要二进制7位编码表示。可以看出每个量化级是不均匀的。在小信号的量化台阶很小，使小信号时量化噪声减小。如果按均匀量化计算，以台阶 
为单位，信号需用L=128X16=2048= 
个量化级表示，既需要11位编码。这样非均匀编码使小信号量化台阶缩小了16倍，相当于小信号信噪比改善了20dB。
第三步：把y轴均匀划分为8段，每段均匀分为16分。这样y也分为128个量化级，与x轴的128个量化级对应。因此，压扩特性各段的斜率 
是不同的。段斜率 
其他段为: 
。
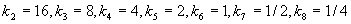
以上分段为x取正值时的情况。而x取负值时，压扩特性与x取正值成奇对称。在正8段和负8段中，正1，2段和负1，2段斜率相同，合为一段。所以原来的16段折线变为13段折线。
